多方计算

开坑后一定更有动力写！

GG18

原论文：Fast Multiparty Threshold ECDSA with Fast Trustless Setup。

目标

注意：上述签名方式与标准流程略有区别（ $r=g^k$ 表达为 $r=g^{k^{-1}}$ ， $s$ 处相反），应该是为了求 $s$ 时更好维护。

原理

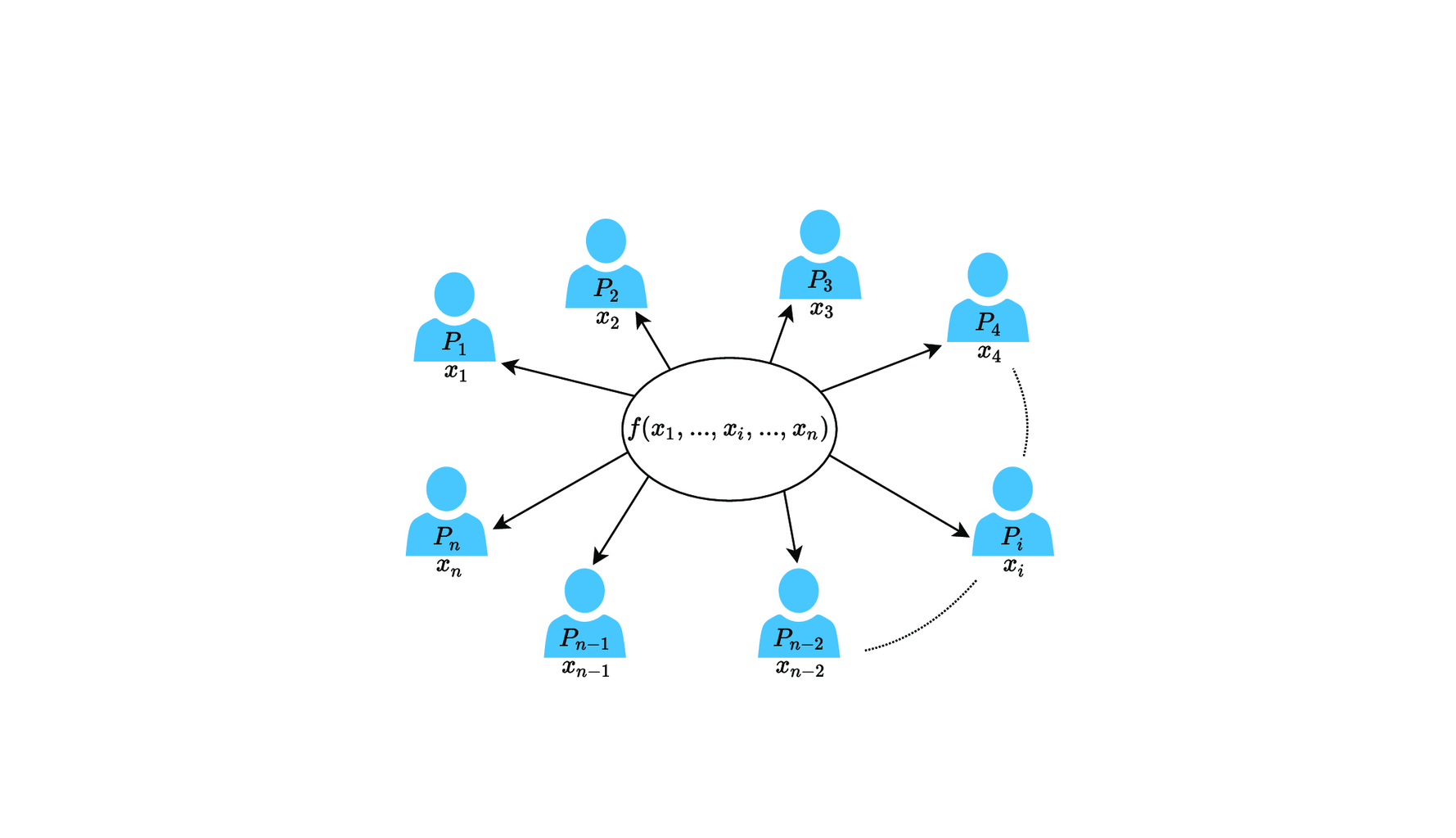
将私钥 $x$ 和每次签名的随机数 $k$ 各自拆成 $\sum x_i$ 和 $\sum k_i$ ，每个参与者都持有一份。

求 $r=g^{k^{-1}}$ 时引入辅助随机数 $\gamma=\sum \gamma_i$ ，同样由每个参与者生成并持有一份：

$\begin{aligned} g^{k^{-1}}&=g^{\gamma k^{-1} \gamma^{-1}} \\ &=\left(g^{\sum \gamma_i} \right)^{(k\gamma)^{-1}} \\ &=\left(\prod g^{\gamma_i} \right)^{(k\gamma)^{-1}} \end{aligned}$

注意到各自公开 $g^{\gamma_i}$ 不影响 $\gamma_i$ 的安全性，只需优雅计算出 $k \gamma$ 即可。

求 $k\gamma$ 时，每一组参与者 $(i,j)$ 需要用 MtA 将 $k_i\gamma_j$ 拆解为各自持有的 $k_i\gamma_j=\alpha_{i,j}+\beta_{i,j}$

$\begin{aligned} kv&=\left(\sum k_i\right)\left(\sum \gamma_i \right) \\ &=\sum\limits_{i \ne j}k_i \gamma_j+\sum k_i\gamma_i \\ &=\sum\limits_{i \ne j}(\alpha_{i,j}+\beta_{i,j})+\sum k_i\gamma_i \\ &=\sum \left(k_i\gamma_i+\sum_{j \ne i} \alpha_{i,j} +\sum_{j \ne i} \beta_{j, i}\right) \end{aligned}$

计算 $s$ 时，每一组参与者 $(i,j)$ 同样用 MtA 将 $k_ix_j$ 拆解为 $k_ix_j=\mu_{i,j}+\nu_{i,j}$

$s=k(m+xr)=\left(\sum k_i\right)m+\left(\sum k_i\right)\left(\sum x_i\right)r=\sum (mk_i+r\sigma_i)$

MtA 协议

Multiplicative-to-Additive 指的是乘法到加法的转换协议。假设 Alice 和 Bob 各自有个秘密值 $a \in \mathbb{Z}_q,b \in \mathbb{Z}_q$ ，MtA 能在不泄露各自秘密的情况下，让他们各自得到 $\alpha \in \mathbb{Z}_q,\beta \in \mathbb{Z}_q$ 使得 $ab=\alpha+\beta \mod q$ 。