本文会重点基于 ECDSA 的场景介绍安全多方计算框架下的门限签名：

  • 安全多方计算（Secure Multi-Party Computation）是一种隐私计算技术，用于多方在不泄露私有输入的情况下计算任意函数。常见概念包括：秘密分享、不经意传输、混淆电路、同态加密等。
  • 门限签名（Threshold Signature Scheme）是一种加密数字签名协议，是安全多方计算的实际应用场景。通常用 (t,n)(t,n) 表达：密钥散布在 nn 个人手里，<t< t 个人一定无法签名成功，但任意 ≥t\ge t 个人一定能签名成功。

前置知识

Shamir’s Secret Sharing

1979 年 Shamir 在 How to share a secret 中提出。

目标：在门限 (t,n)(t,n) 中分享秘密，即 nn 个人各自持有部分秘密，任意 tt 个人能还原出完整秘密。

原理：秘密是多项式 f(x)=a0+a1x+⋯+at−1xt−1f(x)=a_0+a_1x+\dots+a_{t-1}x^{t-1} 中的 a0a_0，每次还原时利用拉格朗日插值。

注意：初始时依赖可信赖第三方（Dealer）生成多项式并分发 (x,f(x))(x,f(x))。

Fiat-Shamir Heuristic

1986 年 Fiat 和 Shamir 在 How to Prove Yourself: Practical Solutions to Identification and Signature Problems 中提出。

目标：零知识证明（Zero-Knowledge Proof）转为非交互式版本（Non-Interactive Zero-Knowledge Proof）。

原理：把交互式协议中 Verifier 的挑战通过哈希函数来自行生成。

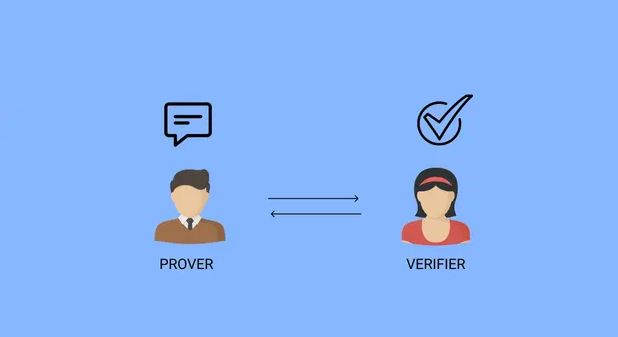
Schnorr Identification Protocol

1989 年 Schnorr 在 Efficient Identification and Signatures for Smart Cards 中提出。

目标：设有限域 Zq\mathbb{Z}_q 下的生成元是 gg，Prover 想在不泄露 α\alpha 的情况下证明他知道 α\alpha 满足 y=gαmod  py=g^{\alpha} \mod p。

原理：

  1. 承诺（Commit）：Prover 随机选择 k∈Zqk \in \mathbb{Z}_q，计算 r=gkmod  pr=g^k \mod p 发送给 Verifier。
  2. 挑战（Challenge）：Verifier 随机选择 e∈Zqe \in \mathbb{Z}_q 并发送给 Prover。
  3. 响应（Response）：Prover 计算 z=k+e⋅αmod  pz=k+e \cdot \alpha \mod p 并发送给 Verifier。
  4. 验证（Verify）：Verifier 检查 gz=?r⋅yeg^z \stackrel{?}{=} r \cdot y^e 是否成立。

Feldman Verifiable Secret Sharing

1987 年 Feldman 在 A Practical Scheme for Non-interactive Verifiable Secret Sharing 中提出。

目标：在门限 (t,n)(t,n) 分享秘密的基础上，保证了 Dealer 在分发 (x,f(x))(x,f(x)) 时无法恶意替换。

原理：

  • Dealer 在分发的同时声明 c0=ga0,c1=ga1,…,ct−1=gat−1c_0=g^{a0},c_1=g^{a_1},\dots,c_{t-1}=g^{a_{t-1}}。
  • 每个成员收到 (x,f(x))(x,f(x)) 后验证 gf(x)=∏icixig^{f(x)}=\prod_i c_i^{x^i} 是否成立。

Pedersen Commitment & Pedersen Verifiable Secret Sharing

1991 年 Pedersen 在 Non-Interactive and Information-Theoretic Secure Verifiable Secret Sharing 中提出。

Pedersen Commitment 目标：Prover 想针对事先不公开的值 α\alpha 提交承诺，使得公开后可验证不可篡改。

Pedersen Commitment 原理：

  • 承诺（Commit）：Prover 随机选择盲化因子 r∈Zqr \in \mathbb{Z}_q，计算承诺 C=gαhrmod  pC=g^{\alpha}h^r \mod p 并发送给 Verifier。
  • 打开（Open）：Prover 公开 (α,r)(\alpha,r)，Verifier 验证 C=?gαhrC \stackrel{?}{=} g^{\alpha}h^r。

Pedersen Commitment 评价：

  • 完美隐藏性：满足信息论安全（Information-Theoretic Secure），即不依赖于计算复杂性假设。
  • 计算绑定性：在离散对数困难性下，敌手无法找到 (α′,r′)(\alpha',r') 使得 (α,r),(α′,r′)(\alpha,r),(\alpha',r') 能生成同样的 CC。
  • （加）同态性：注意到 C1⋅C2=gm1+m2hr1+r2C_1 \cdot C_2=g^{m_1+m_2}h_{r_1+r_2}

Pedersen Verifiable Secret Sharing 原理：

  • 新增 g(x)=b0+b1x+⋯+bt−1xt−1g(x)=b_0+b_1x+\dots+b_{t-1}x^{t-1} 这个陪跑多项式，分发时发送 (x,f(x),g(x))(x,f(x),g(x))。
  • Dealer 分发后公布 ci=saitbic_i=s^{a_i}t^{b_i} 作为承诺，成员验证 sf(x)tg(x)=∏icixis^{f(x)}t^{g(x)}=\prod_i c_i^{x^i}。

Distributed Key Generation

VSS 协议中不依赖 Dealer 的密钥分享算法被称为分布式密钥生成技术（Distributed Key Generation）。

1991 年 Pedersen 在 A Threshold Cryptosystem without a Trusted Party 中提出 Pedersen’s DKG。

  • nn 个人各自随机选择一个秘密 uiu_i，密钥 x=∑iuix=\sum_i u_i。
  • 每位参与者把 uiu_i 通过 Feldman VSS t−1t-1 阶多项式分发给其他参与者。记 fj(x)f_j(x) 为表示第 jj 位参与者秘密的多项式，那么第 ii 位参与者最终会收到 f0(i),f1(i),…,fn−1(i)f_0(i),f_1(i),\dots,f_{n-1}(i)，并计算 xi=∑jfj(i)x_i=\sum_j f_{j}(i)。
  • 当 tt 个参与者想要还原私钥时，用他们的 (idi,xidi)(id_i,x_{id_i}) 拼成的多项式在 00 处的值即为密钥 xx。

1999 年 Gennaro 在 Secure distributed key generation for discrete-log based cryptosystems 中提出恶意参与者可能通过特殊构造的贡献值使得 Pedersen’s DKG 协议泄露共享私钥的信息，并初步给了个新方案。

2006 年，Gennaro 在 Secure Distributed Key Generation for Discrete-Log Based Cryptosystems 中正式提出可证明安全的非交互式的 Gennaro’s DKG，引入了零知识证明、双重验证机制和适应性安全。

Multiplicative-to-Additive

目标：乘法到加法的转换协议。假设 Alice 和 Bob 各自有个秘密值 a∈Zq,b∈Zqa \in \mathbb{Z}_q,b \in \mathbb{Z}_q，MtA 能在不泄露各自秘密的情况下，让他们各自得到 α∈Zq,β∈Zq\alpha \in \mathbb{Z}_q,\beta \in \mathbb{Z}_q 使得 ab=α+βmod  qab=\alpha+\beta \mod q。

MtA 通常使用 Paillier 工具，其具有同态加的特性，详见 《密码学导论》。

ECDSA 多方签名原理

目标

设 G\mathbb{G} 是有限域下阶为 qq 的椭圆曲线，gg 是其生成元。私钥是 xx，公钥是 y=gx∈Gy=g^x \in \mathbb{G}。

  • 签名：将待签字符串表示成字符串 m∈Zqm \in \mathbb{Z}_q，取随机数 k∈Zqk \in \mathbb{Z}_q，计算 R=gk−1∈GR=g^{k^{-1}} \in \mathbb{G}，设 rr 是 RR 点在椭圆上的横坐标，计算 s=k(m+xr)mod  qs=k(m+xr) \mod q，称 (R,s)(R,s) 是一组对 mm 的签名。
  • 验签：计算 R′=gms−1mod  qgrs−1mod  q∈GR'=g^{ms^{-1} \mod q}g^{rs^{-1} \mod q} \in \mathbb{G}，判断是否满足 rr 是 R′R' 的横坐标。

上述签名方式与标准流程略有区别（RR 处从 gkg^{k} 改为为 gk−1g^{k^{-1}}，ss 处从 k−1k-1 改为 kk），猜测为了求 ss 时更好维护。

现在假设私钥是被 nn 个参与者各自维护（即 x=∑xix=\sum x_i），他们想基于门限 tt 对 mm 进行签名但不泄露私钥。

原理

密钥生成时每位参与者各自准备 xix_i，认为全局私钥为 x=∑xix=\sum x_i。

每次签名时每位参与者各自取随机数 kik_i，认为全局随机数 k=∑kik=\sum k_i。

求 r=gk−1r=g^{k^{-1}} 时引入辅助随机数 γ=∑γi\gamma=\sum \gamma_i，同样由每个参与者各自生成：

gk−1=gγk−1γ−1=(g∑γi)(kγ)−1=(∏gγi)(kγ)−1\begin{aligned} g^{k^{-1}}&=g^{\gamma k^{-1} \gamma^{-1}} \\ &=\left(g^{\sum \gamma_i} \right)^{(k\gamma)^{-1}} \\ &=\left(\prod g^{\gamma_i} \right)^{(k\gamma)^{-1}} \end{aligned}

注意到各自公开 gγig^{\gamma_i} 不影响 γi\gamma_i 的安全性，只需优雅计算出 kγk \gamma 即可。为了求出 kγk\gamma，每一组参与者 (i,j)(i,j) 需要用 MtA 协议将 kiγjk_i\gamma_j 拆解为 kiγj=αi,j+βi,jk_i\gamma_j=\alpha_{i,j}+\beta_{i,j}，即双方各自持有 αi,j\alpha_{i,j} 和 βi,j\beta_{i,j}。最后每个参与者求出 δi\delta_i：

kγ=(∑ki)(∑γi)=∑i≠jkiγj+∑ikiγi=∑i≠j(αi,j+βi,j)+∑ikiγi=∑i(δi=kiγi+∑j≠iαi,j+∑j≠iβj,i)\begin{aligned} k\gamma&=\left(\sum k_i\right)\left(\sum \gamma_i \right) \\ &=\sum\limits_{i \ne j}k_i \gamma_j+\sum \limits_i k_i \gamma_i \\ &=\sum\limits_{i \ne j}(\alpha_{i,j}+\beta_{i,j})+\sum \limits_i k_i\gamma_i \\ &=\sum \limits_i \left(\delta_i=k_i\gamma_i+\sum_{j \ne i} \alpha_{i,j} +\sum_{j \ne i} \beta_{j, i}\right) \end{aligned}

计算 ss 时，每一组参与者 (i,j)(i,j) 同样用 MtA 将 kixjk_ix_j 拆解为 kixj=μi,j+νi,jk_ix_j=\mu_{i,j}+\nu_{i,j}，最后每个参与者求出 σi\sigma_i 和 sis_i：

s=k(m+xr)=(∑imki)+(∑iki)(∑ixi)r=∑i(si=mki+rσi)σi=kixi+∑j≠iμi,j+∑j≠iνi,js=k(m+xr)=\left(\sum \limits_i mk_i\right)+\left(\sum \limits_i k_i\right)\left(\sum \limits_i x_i\right)r=\sum \limits_i (s_i=mk_i+r\sigma_i) \\ \sigma_i=k_ix_i+\sum \limits_{j \ne i}\mu_{i,j}+\sum \limits_{j \ne i}\nu_{i,j}

GG18 & GG20

原论文：Fast Multiparty Threshold ECDSA with Fast Trustless Setup，鸣谢 sig01 的 讲解。

协议流程

密钥生成阶段

  1. 每个参与者 ii 生成 ui∈Zqu_i \in \mathbb{Z}_q，生成承诺 (KGCi,KGDi)=Com(gui)(KGC_i,KGD_i)=\text{Com}(g^{u_i}) 并广播 KGCiKGC_i 和 Paillier 公钥 EiE_i。
  2. 参与者进行 DKG，即每个参与者基于自身的秘密 uiu_i 进行 (t,n)(t,n) 的 Feldman-VSS，点对点广播结束后计算出属于自己的 xix_i。同时每个参与者广播 KGDiKGD_i，未来签名的私钥是 x=∑iuix=\sum_i u_i，公钥是 y=gx=∏iguiy=g^x=\prod_i g^{u_i}。
  3. 每位参与者 ii 用 ZKP 证明他们知道 xix_i（因为 gxig^{x_i} 是公开的）且同态加密的 Ni=piqiN_i=p_iq_i 中无平方因子。

参与者集合 SS 对消息 mm 的签名阶段

  1. 签名参与者 i∈Si \in S 生成 ki,γi∈Zqk_i,\gamma_i \in \mathbb{Z}_q，计算 [Ci,Di]=Com(gγi)[C_i,D_i]=\text{Com}(g^{\gamma_i}) 并广播 CiC_i。
  2. 每一组签名参与者 (i,j)∈S(i,j) \in S 进行两个 MtA 子协议：
    • MtA：计算 kiγj=αi,j+βi,jk_i\gamma_j=\alpha_{i,j}+\beta_{i,j}。每个签名参与者 i∈Si \in S 生成 δi=kiγi+∑j≠iαi,j+∑j≠iβj,i\delta_i=k_i\gamma_i+\sum_{j \ne i}\alpha_{i,j}+\sum_{j \ne i}\beta_{j,i}。
    • MtAwc：计算 kiwj=μi,j+νi,jk_iw_j=\mu_{i,j}+\nu_{i,j}。每个签名参与者 i∈Si \in S 生成 σi=kixi+∑j≠iμi,j+∑j≠iνj,i\sigma_i=k_ix_i+\sum_{j \ne i}\mu_{i,j}+\sum_{j \ne i}\nu_{j,i}。
  3. 签名参与者 i∈Si \in S 广播 δi\delta_i，大家可以共同还原出 δ=∑i∈Sδi=kγ\delta=\sum_{i \in S}\delta_i=k\gamma，并计算 δ−1\delta^{-1}。
  4. 签名参与者 i∈Si \in S 广播 DiD_i，大家可以共同还原出 R=g(∑i∈Sγi)δ−1=gk−1R=g^{(\sum_{i \in S}\gamma_i)\delta^{-1}}=g^{k^{-1}} 并计算 r=H′(R)r=H'(R)。
  5. 签名参与者 i∈Si \in S 计算 si=mki+rσis_i=mk_i+r\sigma_i，则签名值满足 s=∑i∈Ss=\sum_{i \in S}。为了安全性增加步骤：
    1. 签名参与者 i∈Si \in S 生成 ℓi,γi∈Zq\ell_i,\gamma_i \in \mathbb{Z}_q 计算 Vi=Rsigℓi,Ai=gρi,[C^i,D^i]=Com(Vi,Ai)V_i=R^{s_i}g^{\ell_i},A_i=g^{\rho_i},[\hat{C}_i,\hat{D}_i]=\text{Com}(V_i,A_i) 并广播 D^i\hat{D}_i。
    2. 签名参与者 i∈Si \in S 用 ZKP 证明他知道 (si,ℓi,ρi)(s_i,\ell_i,\rho_i) 使得 Vi=Rsigℓi,Ai=gρiV_i=R^{s_i}g^{\ell_i},A_i=g^{\rho_i}（如果证明失败则流程结束）。设 ρ=∑i∈Sρi,ℓ=∑i∈Sℓi,A=∏i∈SAi\rho=\sum_{i \in S}\rho_i,\ell=\sum_{i\in S}\ell_i,A=\prod_{i \in S}A_i，那么 V=g−my−r∏i∈SViV=g^{-m}y^{-r}\prod_{i \in S}V_i 满足 V=glV=g^l。
    3. 签名参与者 i∈Si \in S 计算 Ui=Vρi,Ti=Aℓi,[C~i,D~i]=Com(Ui,Ti)U_i=V^{\rho_i},T_i=A^{\ell_i},[\tilde{C}_i,\tilde{D}_i]=\text{Com}(U_i,T_i) 并广播 C~i\tilde{C}_i。
    4. 签名参与者 i∈Si \in S 广播 D~i\tilde{D}_i。大家验证 ∏i∈SUi=?∏i∈STi\prod_{i\in S}U_i \stackrel{?}{=} \prod_{i\in S}T_i，若失败则协议终止。
    5. 经过上述步骤验证后，签名参与者 i∈Si \in S 就可以广播 sis_i 了，签名值满足 s=∑i∈Ssis=\sum_{i \in S}s_i。

Range Proof

GG18 在签名过程中需要对 MtA 子协议进行 Range Proof：利用 Paillier 加密算法来实现 MtA 协议，Bob 计算得到的 α=ab−βmod  N\alpha=ab-\beta \mod N 是基于 Paillier 的公钥取模的，而我们希望这个结果能在模 qq 域下保持正确。

GG18 核心逻辑是 控制数值范围防止对 NN 取模。Alice 把计算公式改为加：Enc(a)⊗b+Enc(β′)Enc(a) \otimes b+Enc(\beta')，注意本地使用 β=−β′mod  q\beta=-\beta' \mod q，这样能在模 qq 域下保持 MtA 结果的准确性。如果 (a,b,β′)(a,b,\beta') 在数值上能保证 ab+β′<Nab+\beta'<N，那么 Paillier 流程相当于没有执行 mod  N\mod N 行为，Bob 解开后的 α\alpha 一定是模 qq 域下正确的。

GG18 为了确保 ab+β′<Nab+\beta'<N 成立，要求 N>q8N>q^8（密钥生成阶段检查），a<q3a<q^3（Alice 生成时保证且声明），b<q3,β′<q7b<q^3,\beta'<q^7（Bob 生成时保证且声明）。这样就有 ab+β′<q3⋅q3+q7<q8<Nab+\beta'<q^3 \cdot q^3+q^7<q^8<N。

在区块链实践中， qq 是 Secp256k1 的 order，256 比特位长度；NN 是 2048 比特位长度。

GG20

安全性问题

CMP20

原论文：UC Non-Interactive, Proactive, Threshold ECDSA

Range Proof 细节

enc：(N0,K)(N_0,K)，证明 ∃k∈±2l\exist k \in \pm 2^l 使得 K=Paillier(k;ρ,N0)K=Paillier(k;\rho,N_0) 。

aff-p：(N0,N1,D,C,Y,X)(N_0,N_1,D,C,Y,X)，证明 ∃x∈±2l,y∈±2l′\exists x \in \pm 2^l,y \in \pm 2^{l'} 使得

X=Paillier(x;ρx,N1),Y=Paillier(y;ρy,N1),D=Cx⋅Paillier(y;ρ,N0)mod  N02X=Paillier(x;\rho_x,N_1),Y=Paillier(y;\rho_y,N_1),D=C^x \cdot Paillier(y;\rho,N_0) \mod N_0^2

aff-g：(Gq,g,N0,N1,C,D,Y,X)(\mathbb{G}_q, g, N_0, N_1, C, D, Y, X)，证明 ∃x∈±2l,y∈±2l′\exists x \in \pm 2^l,y \in \pm 2^{l'} 使得：

gx=X∈G,Y=Paillier(y;ρ1,N1),D=Cx⋅Paillier(y;ρ0,N0)mod  N02g^x=X \in \mathbb{G},Y=Paillier(y;\rho_1,N_1),D=C^x \cdot Paillier(y;\rho_0,N_0) \mod N_0^2

log：(Gq,g,N0,C,X)(\mathbb{G}_q, g, N_0, C, X)，证明 ∃x∈±2l\exist x \in \pm 2^l 使得 C=Paillier(x;ρ,N0),X=gxC=Paillier(x;\rho,N_0),X=g^x 。

协议流程

CGCMP

这篇论文的形成有一段佳话：Rosario Gennaro 和 Steven Goldfeder 在 CCS 2020 提出了 GG20，而 Ran Canetti、Nikolaos Makriyannis、Udi Peled 同样在 CCS2020 提出了 CMP20；双方在 2021 年合作提出了 CGCMP，里面提供了具有 trade-off 的两个签名方法；双方在 2024 年更新了 CGCMP，统一了签名方法。

标题 备注
Fast Multiparty Threshold ECDSA with Fast Trustless Setup GG18，两个作者
One Round Threshold ECDSA with Identifiable Abort GG20，两个作者
UC Non-Interactive, Proactive, Threshold ECDSA CMP20，三个作者
UC Non-Interactive, Proactive, Threshold ECDSA with Identifiable Aborts CGCMP，五个作者
UC Non-Interactive, Proactive, Distributed ECDSA with Identifiable Aborts CGCMP 更新，五个作者