Undecidable Problems
罗素悖论(Russell’s Paradox)是一个很著名的悖论:设集合 S S S S = { x ∣ x ∉ x } S=\{x|x \notin x\} S = { x ∣ x ∈ / x } S S S S S S
我们通常用理发师悖论(The Barber paradox)去解释罗素悖论。假设城里只有一个理发师,且任何一个不能自己理发的人会由理发师帮他理发。定义 S ( x ) S(x) S ( x ) x x x S ( b a r b e r ) = { x ∣ x ∉ S ( x ) } S(barber)=\{x|x \notin S(x)\} S ( ba r b er ) = { x ∣ x ∈ / S ( x )} b a r b e r ∈ S ( b a r b e r ) barber \in S(barber) ba r b er ∈ S ( ba r b er )
经典的停机问题(Halting problem)就是从以上的悖论中构造出来的。于是我们用 Undecidable Problem 去描述那些不存在算法能正确判定 yes/no 的问题。判定两个 CFG 是否同构也是不能解的。
下面介绍一下 Post Correspondence Problem。给出一个 dominos 集合,每一个 domino 的上下部分各印有一个字符串,且可以翻转。现在要找一个有限的 domino 序列(每一种 domino 可以重复选),使得上下部分各自连成的字符串完全相同。左图展示了 4 4 4
那么是否存在一种算法能判定一个 PCP 实例的解的存在性?答案是否定的。当字符集 ≥ 2 \ge 2 ≥ 2
Merge-Insertion-Sort
先从一个问题引入:有 N N N
首先,基于比较 的排序算法的复杂度下界是 O ( N log N ) O(N \log N) O ( N log N ) N ! N! N ! O ( log N ! ) = O ( N log N ) O(\log{N!})=O(N\log N) O ( log N ! ) = O ( N log N )
可是归并排序也只需 O ( N log N ) O(N \log N) O ( N log N ) 精确步数 ,而非在大 O O O N N N
一个经典且有效的策略是 Binary Comparison Sort :每次把第 k k k k − 1 k-1 k − 1 ∑ k = 1 N ⌈ log 2 k ⌉ \sum \limits_{k=1}^N \lceil \log_2k \rceil k = 1 ∑ N ⌈ log 2 k ⌉
上述做法在 N = 5 N=5 N = 5 8 8 8 7 7 7
首先任意挑 4 4 4 5 5 5 b 1 < a 1 , b 2 < a 2 , b 3 b_1<a_1,b_2<a_2,b_3 b 1 < a 1 , b 2 < a 2 , b 3
比较 a 1 a_1 a 1 a 2 a_2 a 2 a 1 < a 2 a_1<a_2 a 1 < a 2
将 b 3 b_3 b 3 b 1 < a 1 < a 2 b_1<a_1<a_2 b 1 < a 1 < a 2 2 2 2
将 b 2 b_2 b 2 ( b 1 , a 1 , b 3 ) (b_1,a_1,b_3) ( b 1 , a 1 , b 3 ) b 2 < a 2 b_2<a_2 b 2 < a 2 2 2 2
Merge-Insertion-Sort 从这个例子受到启发进行递归设计的,具体操作如下:
首先将数字分成 ⌊ N / 2 ⌋ \lfloor N/2 \rfloor ⌊ N /2 ⌋ b i < a i ( i ∈ 1.. N ) b_i<a_i(i \in 1..N) b i < a i ( i ∈ 1.. N ) b N / 2 + 1 b_{N/2+1} b N /2 + 1
对于 a a a N / 2 N/2 N /2
依次把 b b b 2 2 2 b 3 , b 2 b_3,b_2 b 3 , b 2 ( b 1 , a 1 , a 2 ) (b_1,a_1,a_2) ( b 1 , a 1 , a 2 ) 3 3 3 b 5 , b 4 b_5,b_4 b 5 , b 4 4 4 4 b 11 ∼ b 6 b_{11}\sim b_6 b 11 ∼ b 6
现在我们来分析一下 Merge-Insertion-Sort 的具体步数。
设 F ( N ) F(N) F ( N ) N N N F ( N ) = ⌊ N / 2 ⌋ + F ( ⌊ N / 2 ⌋ ) + G ( ⌊ N / 2 ⌋ ) F(N)=\lfloor N/2 \rfloor+F(\lfloor N/2 \rfloor)+G(\lfloor N/2 \rfloor) F ( N ) = ⌊ N /2 ⌋ + F (⌊ N /2 ⌋) + G (⌊ N /2 ⌋) G ( N ) G(N) G ( N ) N N N
下面我们来计算一下 G ( N ) G(N) G ( N ) ( 0 , 2 , 2 , 6 , 10 , … ) (0,2,2,6,10,\dots) ( 0 , 2 , 2 , 6 , 10 , … ) ( 1 , 1 , 3 , 5 , 11 , … ) (1,1,3,5,11,\dots) ( 1 , 1 , 3 , 5 , 11 , … ) t k − 1 + t k = 2 k t_{k-1}+t_k=2^k t k − 1 + t k = 2 k
若 t k − 1 ≤ m ≤ t k , G ( m ) = ( t 1 − t 0 ) + 2 ( t 2 − t 1 ) ⋯ + k ( m − t k − 1 ) = k m − ∑ t i t_{k-1} \le m \le t_k,G(m)=(t_1-t_0)+2(t_2-t_1) \dots +k(m-t_{k-1})=km-\sum t_i t k − 1 ≤ m ≤ t k , G ( m ) = ( t 1 − t 0 ) + 2 ( t 2 − t 1 ) ⋯ + k ( m − t k − 1 ) = km − ∑ t i
注意到 ∑ i = 0 m − 1 t i = ⌊ 2 k + 1 / 3 ⌋ \sum \limits_{i=0}^{m-1} t_i=\lfloor 2^{k+1}/3 \rfloor i = 0 ∑ m − 1 t i = ⌊ 2 k + 1 /3 ⌋
最后我们可以得到 F ( N ) = ∑ k = 1 N ⌈ log 2 ( 3 k / 4 ) ⌉ F(N)=\sum \limits_{k=1}^N \lceil \log_2(3k/4) \rceil F ( N ) = k = 1 ∑ N ⌈ log 2 ( 3 k /4 )⌉
我们再来考虑一下这个问题的 Lower_bound。总共有 N ! N! N ! Decision Tree )定理我们得到下界是 ⌊ log 2 N ! ⌋ \lfloor \log_2{N!} \rfloor ⌊ log 2 N ! ⌋
下面我们来感受一下 Binary Comparison Sort,Merge-Insertion-Sort 和 Lower_bound 的效果:
算法
4
5
6
7
8
9
10
11
12
LB
5
7
10
13
16
19
22
26
29
MI
5
7
10
13
16
19
22
26
30
BC
5
8
11
14
17
21
25
29
33
Adversary Argument
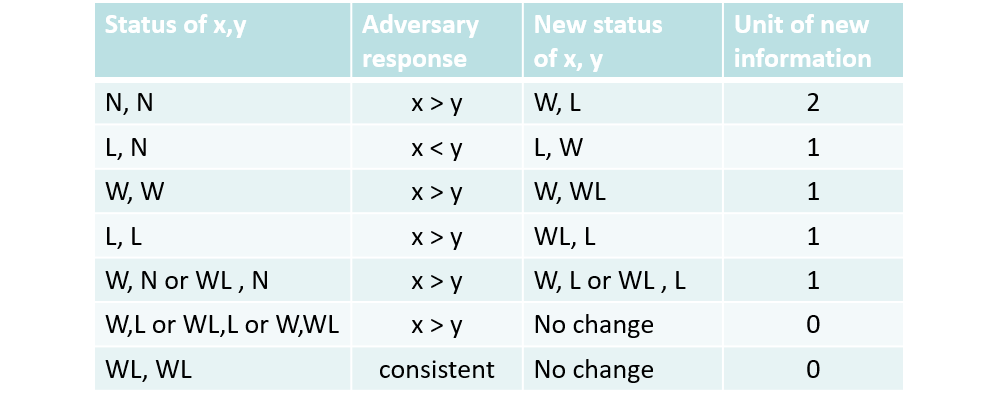
除了 Decision Tree 外,我们有一个强有力的工具 Adversary 来分析一个算法的下界 。它的核心思想是:Release the least information and change the scenario to make the algorithm work hard.
先来考虑一个 Find Second Maximum Element 问题。我们都知道,找最大值至少需要也仅需要 N − 1 N-1 N − 1 2 N − 3 2N-3 2 N − 3
那么如何分析出下界呢?首先我们观察一个很有趣的结论:次大值只能在那些与最大值比较过的数字里产生 。所以该问题的下界其实是 N − 1 + M − 1 N-1+M-1 N − 1 + M − 1 M M M M M M M m i n = min a ∈ A M a M_{min}=\min\limits_{a \in A}M_a M min = a ∈ A min M a 更紧 的下界,我们要找到一种策略,使得它的 M m i n M_{min} M min
现在我们要借助 Adversary 分析出尽量大的 M m i n M_{min} M min
给每一个数字 x x x g ( x ) g(x) g ( x ) g ( x ) = 1 g(x)=1 g ( x ) = 1
假设某一次询问的数对是 ( x , y ) (x,y) ( x , y ) g ( x ) ≥ g ( y ) g(x) \ge g(y) g ( x ) ≥ g ( y ) x > y x>y x > y g ( x ) = g ( x ) + g ( y ) , g ( y ) = 0 g(x) = g(x)+g(y),g(y)=0 g ( x ) = g ( x ) + g ( y ) , g ( y ) = 0
注意到,无论你用什么算法来给出 ( x , y ) (x,y) ( x , y ) g ( x ) g(x) g ( x ) 2 2 2 z z z g ( z ) = N g(z)=N g ( z ) = N z z z ⌈ log N ⌉ \lceil \log N \rceil ⌈ log N ⌉ M m i n = ⌈ log N ⌉ M_{min}=\lceil \log N \rceil M min = ⌈ log N ⌉ Find Second Maximum Element 问题的一个比较次数下界是 N + ⌈ log N ⌉ − 2 N+\lceil \log N \rceil-2 N + ⌈ log N ⌉ − 2 。
再来考虑一个 Median 问题:有 N N N
显然排序问题的比较次数是其上界。那么下界是什么样的呢?想象一棵 N N N
称 ( x , y ) (x,y) ( x , y ) Crucial Comparison ,如果它满足 x > y ≥ m e d i a n x>y \ge median x > y ≥ m e d ian x < y ≤ m e d i a n x<y\le median x < y ≤ m e d ian Non-Crucial Comparison 。可以发现,如果去对应那 N N N
Adversary 提供这样一种策略:使每次询问得到的结果尽量都是 Non-Crucial Comparison。具体地,设状态 N N N S S S L L L ( x , y ) (x,y) ( x , y )
如果状态是 ( N , N ) (N,N) ( N , N ) ( S , L ) (S,L) ( S , L )
如果状态是 ( N , L ) (N,L) ( N , L ) ( N , S ) (N,S) ( N , S ) N N N ( N − 1 ) / 2 (N-1)/2 ( N − 1 ) /2 L L L S S S ( N − 1 ) / 2 (N-1)/2 ( N − 1 ) /2 N − 1 N-1 N − 1 Median 问题的比较次数下界是 3 ( N − 1 ) / 2 3(N-1)/2 3 ( N − 1 ) /2
来看 Median 问题里 N = 5 N=5 N = 5 7 7 7 6 6 6 6 6 6
先花 3 3 3 ( a < b < d , c < d ) (a<b<d,c<d) ( a < b < d , c < d )
此时我们知道 d d d d d d
把 e e e c c c b b b 2 2 2 a < b < e , c < e a<b<e,c<e a < b < e , c < e
最后花 1 1 1 b b b c c c
我们再来设计一种 普适的算法 求解 Median 问题,使得比较次数尽量少。一般化问题,设 S e l e c t ( S , k ) Select(S,k) S e l ec t ( S , k ) S S S k k k W ( N ) W(N) W ( N ) ∣ S ∣ = N |S|=N ∣ S ∣ = N S e l e c t ( S , k ) Select(S,k) S e l ec t ( S , k )
将 S S S 5 5 5 6 ( N / 5 ) 6(N/5) 6 ( N /5 )
递归调用 W W W N / 5 N/5 N /5 m ∗ m^\ast m ∗ W ( N / 5 ) W(N/5) W ( N /5 )
以 m ∗ m^\ast m ∗ S S S S 1 , S 2 S_1,S_2 S 1 , S 2 m ∗ m^\ast m ∗
如果 k ≤ ∣ S 1 ∣ k \le |S_1| k ≤ ∣ S 1 ∣ S e l e c t ( S 1 , k ) Select(S_1,k) S e l ec t ( S 1 , k )
否则调用 S e l e c t ( S 2 , k − ∣ S 1 ∣ − 1 ) Select(S_2,k-|S_1|-1) S e l ec t ( S 2 , k − ∣ S 1 ∣ − 1 )
任何情况下 ∣ S 1 ∣ , ∣ S 2 ∣ ≤ 7 N / 10 |S_1|,|S_2| \le 7N/10 ∣ S 1 ∣ , ∣ S 2 ∣ ≤ 7 N /10 W ( N ) = 6 N / 5 + W ( N / 5 ) + 2 N / 5 + W ( 7 N / 10 ) W(N)=6N/5+W(N/5)+2N/5+W(7N/10) W ( N ) = 6 N /5 + W ( N /5 ) + 2 N /5 + W ( 7 N /10 )
可以用数学归纳法证明 W ( N ) ≤ 16 N W(N) \le 16N W ( N ) ≤ 16 N Median 问题的比较次数上界是 16 N 16N 16 N 。
再来看一个 Find Max and Min 问题。 一个很优秀的分治做法是:
设 f ( S ) f(S) f ( S ) S S S
如果 ∣ S ∣ = 2 |S|=2 ∣ S ∣ = 2
若 ∣ S ∣ > 2 |S| > 2 ∣ S ∣ > 2 S 1 S_1 S 1 S 2 S_2 S 2 f ( S 1 ) f(S_1) f ( S 1 ) f ( S 2 ) f(S_2) f ( S 2 ) max \max max min \min min T ( N ) = 2 T ( N / 2 ) + 2 T(N)=2T(N/2)+2 T ( N ) = 2 T ( N /2 ) + 2
最后解得 T ( N ) = ⌈ 3 2 N ⌉ − 2 T(N)=\lceil \frac{3}{2}N \rceil-2 T ( N ) = ⌈ 2 3 N ⌉ − 2
定义四种状态 ( N , W i n , L o s s , B o t h ) \mathrm{(N,Win,Loss,Both)} ( N , Win , Loss , Both ) N \mathrm{N} N W / L \mathrm{W/L} W/L N − 2 N-2 N − 2 W / L \mathrm{W/L} W/L B \mathrm{B} B 2 N − 2 2N-2 2 N − 2
如果比较 ( N , N ) \mathrm{(N,N)} ( N , N ) 2 2 2 ( W , L ) \mathrm{(W,L)} ( W , L )
如果比较 ( N , W ) \mathrm{(N,W)} ( N , W ) W \mathrm{W} W 1 1 1 ( L , W ) \mathrm{(L,W)} ( L , W )
如果比较 ( W , L / B ) \mathrm{(W,L/B)} ( W , L/B )
如果比较 ( W , W ) \mathrm{(W,W)} ( W , W ) 1 1 1 ( W , B ) \mathrm{(W,B)} ( W , B )
至多有 N / 2 N/2 N /2 2 2 2 N − 2 N-2 N − 2 ⌈ 3 2 N ⌉ − 2 \lceil \frac{3}{2}N \rceil-2 ⌈ 2 3 N ⌉ − 2
再看一个 Find x in Matrix 问题:有一个 N × N N \times N N × N x x x > , < , = >,<,= > , < , =
考虑这样一个算法:从右上角开始询问,假设当前的数字是 e e e e < x e < x e < x e > x e > x e > x x x x 2 N − 1 2N-1 2 N − 1
现在用 Adversary 证明这就是下界。
1 2 3 4 5 6 8 2 3 4 5 6 8 6 3 4 5 6 8 6 5 4 5 6 8 6 5 4 5 6 8 6 5 4 3 6 8 6 5 4 3 2 8 6 5 4 3 2 1 \begin{matrix} 1 & 2 & 3 & 4 & 5 & 6 & 8 \\ 2 & 3 & 4 & 5 & 6 & 8 & 6 \\ 3 & 4 & 5 & 6 & 8 & 6 & 5 \\ 4 & 5 & 6 & 8 & 6 & 5 & 4 \\ 5 & 6 & 8 & 6 & 5 & 4 & 3 \\ 6 & 8 & 6 & 5 & 4 & 3 & 2 \\ 8 & 6 & 5 & 4 & 3 & 2 & 1\end{matrix}
1 2 3 4 5 6 8 2 3 4 5 6 8 6 3 4 5 6 8 6 5 4 5 6 8 6 5 4 5 6 8 6 5 4 3 6 8 6 5 4 3 2 8 6 5 4 3 2 1
上述矩阵给出了一个形式化构造(以 N = 7 N=7 N = 7 6 6 6 8 8 8 7 7 7 x x x N × N N \times N N × N 2 N − 1 2N-1 2 N − 1
再来看一个 Merge Sorted Sequence 问题。将两个长度为 N N N 2 N − 1 2N-1 2 N − 1
构造数列 X , Y X,Y X , Y Y i < X j Y_i<X_j Y i < X j i < j i<j i < j X i = 2 i − 1 , Y i = 2 i X_i=2i-1,Y_i=2i X i = 2 i − 1 , Y i = 2 i X 1 , Y 1 , X 2 , … , X n , Y n X_1,Y_1,X_2,\dots,X_n,Y_n X 1 , Y 1 , X 2 , … , X n , Y n 2 N − 2 2N-2 2 N − 2 i i i
如果 i ≥ 2 i \ge 2 i ≥ 2 X i X_i X i Y i Y_i Y i Y i + 1 Y_{i+1} Y i + 1
如果 i = 1 i=1 i = 1 X 1 X_1 X 1 Y 1 Y_1 Y 1
现在我们把 X i X_i X i Y i Y_i Y i 2 N − 1 2N-1 2 N − 1
Unbound Searching
假设有这样一个定义在正整数域上的函数 F ( x ) F(x) F ( x )
F ( x ) = { 0 0 < x < N 1 x ≥ N F(x)=\left\{ \begin{aligned} & 0 \quad &0<x<N \\ & 1 \quad &x \ge N \end{aligned} \right.
F ( x ) = { 0 1 0 < x < N x ≥ N
如何用最少的步数来确定 N N N
最先想到的肯定是二分,但是这个问题里 N N N + ∞ +\infty + ∞
定义 Binary search B 1 B_1 B 1
从小到大询问 F ( 2 i − 1 ) F(2^i-1) F ( 2 i − 1 ) F ( 1 ) , F ( 3 ) , F ( 7 ) , … F(1),F(3),F(7),\dots F ( 1 ) , F ( 3 ) , F ( 7 ) , … F ( 2 m − 1 ) = 1 F(2^m-1)=1 F ( 2 m − 1 ) = 1
现在我们知道 N ≤ 2 m − 1 N \le 2^m-1 N ≤ 2 m − 1 m = ⌊ log 2 N ⌋ + 1 m = \lfloor \log_2N \rfloor + 1 m = ⌊ log 2 N ⌋ + 1
在 [ 2 m − 1 , 2 m − 1 ) [2^{m-1},2^m-1) [ 2 m − 1 , 2 m − 1 ) ⌊ log 2 N ⌋ \lfloor \log_2N \rfloor ⌊ log 2 N ⌋
总步数 S B 1 = 2 ⌊ log 2 N ⌋ + 1 S_{B_1}=2\lfloor \log_2N \rfloor + 1 S B 1 = 2 ⌊ log 2 N ⌋ + 1
可不可以做得更好呢?我们可以用迭代的方法更快地算出 m m m
定义 Double Binary search B 2 B_2 B 2
套用 B 1 B_1 B 1 m m m 2 ⌊ log 2 m ⌋ + 1 2 \lfloor \log_2m \rfloor+1 2 ⌊ log 2 m ⌋ + 1
重复 B 1 B_1 B 1 2 ∼ 3 2\sim3 2 ∼ 3 S B 2 = ⌊ log 2 N ⌋ + 2 ⌊ log 2 ( ⌊ log 2 N ⌋ + 1 ) ⌋ + 1 S_{B_2}=\lfloor \log_2N \rfloor + 2 \lfloor \log_2(\lfloor \log_2N \rfloor+1) \rfloor + 1 S B 2 = ⌊ log 2 N ⌋ + 2 ⌊ log 2 (⌊ log 2 N ⌋ + 1 )⌋ + 1
那么对于 k-Binary Search B k B_k B k S B k ( N ) = L 1 ( N ) + L 2 ( N ) + ⋯ + L k − 1 ( N ) + 2 L k ( N ) + 1 S_{B_k}(N) = L^1(N) + L^2 (N) + \dots + L^{k-1}(N) + 2L^k (N) +1 S B k ( N ) = L 1 ( N ) + L 2 ( N ) + ⋯ + L k − 1 ( N ) + 2 L k ( N ) + 1
现在还有一个问题:如何找出我们想要的 k k k g ( n ) g(n) g ( n )
g ( n ) = { 2 n = 1 2 g ( n − 1 ) − 1 n ≥ 2 g(n)=\left\{ \begin{aligned} & 2 \quad &n=1 \\ & 2^{g(n-1)}-1 \quad &n \ge 2 \end{aligned} \right.
g ( n ) = { 2 2 g ( n − 1 ) − 1 n = 1 n ≥ 2
我们从小到大尝试 g g g F ( g ( k ) ) = 1 F(g(k))=1 F ( g ( k )) = 1
Reduction
Reduction 是个经典的话题。来看一个经典的 Integer Distinctness Problem 。
给出一个数的集合 { x 1 , x 2 , … , x n } \{x_1,x_2,\dots,x_n\} { x 1 , x 2 , … , x n }
显然可以通过 sorting 解决这个问题。神奇的是,我们可以反过来证明 sorting ∝ \propto ∝ IDP 。
假设 x x x ( x i , x i + 1 ) (x_i,x_{i+1}) ( x i , x i + 1 ) x j x_j x j x j + 1 x_{j+1} x j + 1 x j x_j x j x j + 1 x_{j+1} x j + 1
现在我们开始规约。本来手里有一个 sorting 问题,我们先求解这个序列的 IDP 问题。
求解 IDP 过程中涉及了若干次比较。把这些比较的结果都保留下来,建成一个有向拓扑图,最后对其跑线性的拓扑排序。由结论 1 1 1
所以我们用了和求解 IDP 一样的复杂度,把 sorting 规约到了 IDP。
再来看一个连续规约的例子:3-SUM ∝ \propto ∝ ∝ \propto ∝ 。
3-SUM 问题:有 N N N ( a , b , c ) (a,b,c) ( a , b , c ) a + b + c = 0 a+b+c=0 a + b + c = 0
Collinearity 问题:平面上有 N N N
Segment Splitting 问题:平面上有 N N N
3-SUM ∝ \propto ∝ a a a ( a , a 3 ) (a,a^3) ( a , a 3 ) a + b + c = 0 a+b+c=0 a + b + c = 0 ( b 3 − a 3 , b − a ) × ( c 3 − a 3 , c − a ) = 0 (b^3-a^3,b-a) \times (c^3-a^3,c-a)=0 ( b 3 − a 3 , b − a ) × ( c 3 − a 3 , c − a ) = 0 a a a ( a , 0 ) , ( a , 2 ) , ( − a 2 , 1 ) (a,0),(a,2),(-\frac{a}{2},1) ( a , 0 ) , ( a , 2 ) , ( − 2 a , 1 ) a + b + c = 0 a+b+c=0 a + b + c = 0 ( a , 2 ) , ( − b 2 , 1 ) , ( c , 0 ) (a,2),(-\frac{b}{2},1),(c,0) ( a , 2 ) , ( − 2 b , 1 ) , ( c , 0 ) ( a , b , c ) (a,b,c) ( a , b , c )
Collinearity ∝ \propto ∝ y = 0 , 1 , 2 y=0,1,2 y = 0 , 1 , 2 a a a
因为 3-SUM 是很多问题简化版本,对其的研究突破至关重要。可惜的是,人们已经证明:对于任何一个 ϵ > 0 \epsilon > 0 ϵ > 0 O ( N 2 − ϵ ) O(N^{2-\epsilon}) O ( N 2 − ϵ )
3-SUM 还有一个变种问题 3-SUM’:选数时可以重复选,即 a , b , c a,b,c a , b , c 3-SUM’ ∝ \propto ∝ 3-SUM :对于 3-SUM’ 里的每个数 x x x { a , a − 3 m a x , a + 3 m a x } \{a,a-3max,a+3max\} { a , a − 3 ma x , a + 3 ma x } m a x max ma x
再来看一个厉害的 Reduction:矩阵乘法和矩阵求逆是可以相互规约的 。这里只证明前者规约后者。对于矩阵乘法 A × B A \times B A × B O ( N 2 ) O(N^2) O ( N 2 ) 3 N × 3 N 3N \times 3N 3 N × 3 N A B AB A B
D = ( I n A 0 0 I n B 0 0 I n ) D − 1 = ( I n − A A B 0 I n − B 0 0 I n ) D=
\begin{pmatrix}
I_n & A & 0 \\
0 & I_n & B \\
0 & 0 & I_n
\end{pmatrix}
\quad
D^{-1}=
\begin{pmatrix}
I_n & -A & AB \\
0 & I_n & -B \\
0 & 0 & I_n
\end{pmatrix}
D = I n 0 0 A I n 0 0 B I n D − 1 = I n 0 0 − A I n 0 A B − B I n
Flow and Match
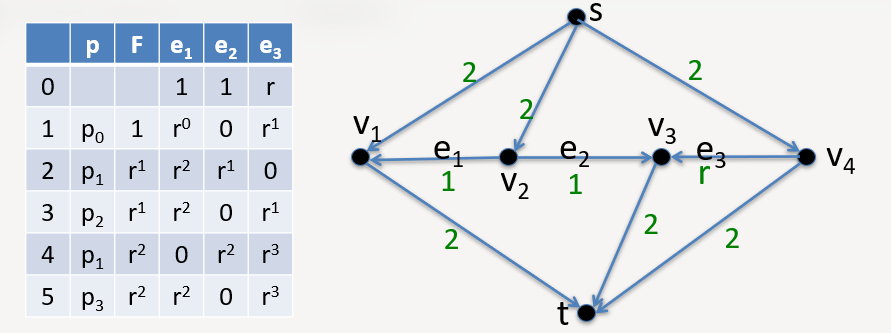
Ford-Fulkerson 算法是最朴素的最大流算法:每次任意找一条增广路进行增广。值得注意的是,该算法可能永远也不会停止,下图就是一个例子。r 2 = 1 − r , r = 5 – 1 2 ≃ 0.618 r^2 = 1 - r, r=\frac{\sqrt 5 – 1}{2}\simeq 0.618 r 2 = 1 − r , r = 2 5 –1 ≃ 0.618 1 + 2 ( r 1 + r 2 + r 3 + … ) = 3 + 2 r < 5 1 + 2(r^1 + r^2+ r^3 + …)=3+2r<5 1 + 2 ( r 1 + r 2 + r 3 + … ) = 3 + 2 r < 5
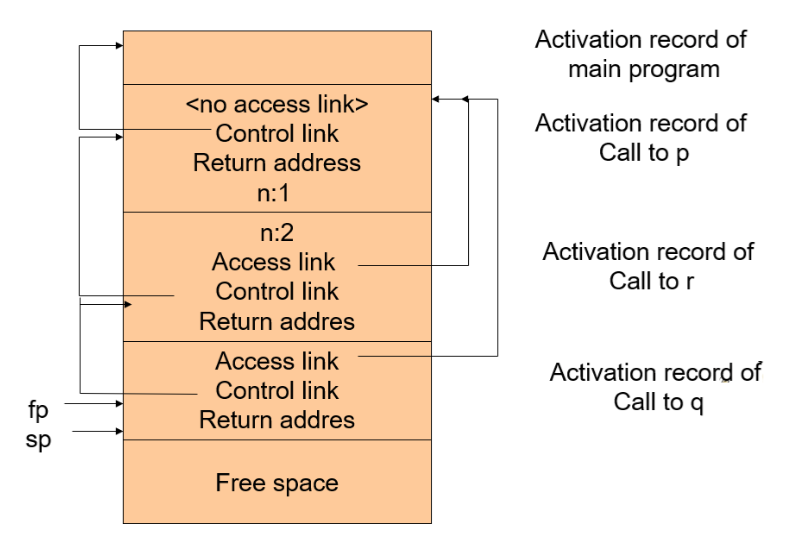
Edmonds-Karp Algorithm 算法改进了上述过程。它先用 BFS 对点进行标号,每次选择最短的增广路。一条增广路上至少存在一条边 e = ( u , v ) e=(u,v) e = ( u , v ) 1 1 1 N N N M M M O ( M ) O(M) O ( M ) O ( N M 2 ) O(NM^2) O ( N M 2 )
我们熟知的 Dinic 算法其实是 EK 算法的多路增广版本。Dinic 引入了分层机制——每次把到终点距离相同的最短路径同时增广,使得复杂度降成 O ( N 2 M ) O(N^2M) O ( N 2 M ) N \sqrt N N
我们用 V i V_i V i i i i
假设最终的最大流是 f f f ∣ V i ∣ ≥ f |V_i| \ge f ∣ V i ∣ ≥ f
对以上不等式求和。假设起点到终点的距离是 D D D D ≤ ∣ V ∣ / f D \le |V|/f D ≤ ∣ V ∣/ f
如果 f ≤ ∣ V ∣ f \le \sqrt {|V|} f ≤ ∣ V ∣ 1 1 1
如果 f > ∣ V ∣ f > \sqrt{|V|} f > ∣ V ∣ D ≤ ∣ V ∣ D \le \sqrt{|V|} D ≤ ∣ V ∣ 1 1 1 ∣ V ∣ \sqrt{|V|} ∣ V ∣
知乎里 讨论了如何构造出让 Dinic 跑 Θ ( N 2 M ) \Theta(N^2M) Θ ( N 2 M )
说起匹配问题,还不得不提到一个 霍尔定理 。对于左右各 N N N
∀ P ∈ L ∣ R i g h t ( P ) ∣ ≥ ∣ P ∣ ⇔ |Match(L,R)|=|L|=|R| \forall_{P \in L}|Right(P)| \ge |P| \Leftrightarrow \text{|Match(L,R)|=|L|=|R|}
∀ P ∈ L ∣ R i g h t ( P ) ∣ ≥ ∣ P ∣ ⇔ |Match(L,R)|=|L|=|R|
右推左是显然。左推右可以反证:考虑网络流跑完的残量网络,取 P P P S S S
Computational Geometry
凸包这个话题想必大家都不陌生。
通过构造点 ( x i , x i 2 ) (x_i,x_i^2) ( x i , x i 2 ) O ( N log N ) O(N\log N) O ( N log N )
因为凸包的计算几何里的应用很广,如何构建凸包是一个脍炙人口的话题。在算法竞赛里,我们一般用 sort +扫两遍分别求上下凸壳的方法,速度快代码短。下面再来介绍几种有趣的构建方法:
Jarvis March - gift wrapping :从下面的点 s s s t t t ( s , t ) (s,t) ( s , t ) t t t O ( N h ) O(Nh) O ( N h )
我们同样熟悉的 Graham Scan 其实就是对上述算法的优化,用极角排序把复杂度降为 O ( N log N ) O(N \log N) O ( N log N )
Quickhull :初始时找到 x x x ( p , q ) (p,q) ( p , q ) r r r ( p , r ) (p,r) ( p , r ) ( q , r ) (q,r) ( q , r ) O ( N log N ) O(N\log N) O ( N log N ) O ( N 2 ) O(N^2) O ( N 2 ) 分治算法 :每次按 x x x O ( N log N ) O(N \log N) O ( N log N )
下面我们再来看一个 Line Segment Intersection 问题:给出平面上的 N N N O ( N 2 ) O(N^2) O ( N 2 )
维护一条垂直于 X 轴的 sweeping line (扫描线)。从左往右扫,保证扫描线左边的交点已经全找到了。这里有一个小结论:最近相交的两条线段,它们一定会与扫描线都有交点,而且这两个交点是 相邻 的。所以我们用平衡树按顺序维护所有与扫描线产生交点的线段。我们再用一个堆维护一些关键节点,包括 一条线段的终点位置 和 两条在扫描线上相邻线段的交点。每次弹出最近的关键节点(把扫描线移到那里),更新扫描线上(平衡树里)的点,同时也更新堆里的点。总复杂度是 O ( ( N + K ) log N ) O((N+K)\log N) O (( N + K ) log N ) K K K
Voronoi Diagram
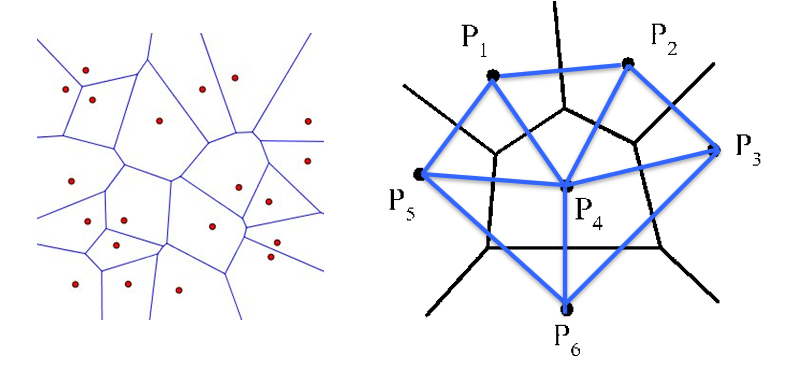
V 图是分析和处理平面图的一个有力的工具,而且他的定义也十分自然。
所谓 V图 ,就是把平面(无限或者有限)分割成若干个部分。初始时有 N N N s k s_k s k C k C_k C k s k s_k s k
结合左图的例子我们还能发现,每一段区域的边界都是一组 ( s i , s j ) (s_i,s_j) ( s i , s j ) s s s s k s_k s k
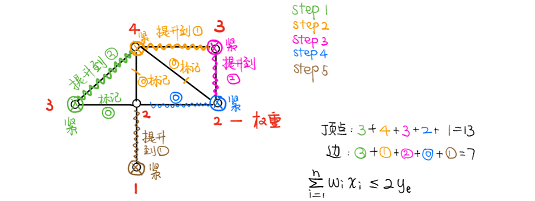
定理:若 N ≥ 3 N \ge 3 N ≥ 3 2 N − 5 2N-5 2 N − 5 3 N − 6 3N-6 3 N − 6
证明:假设有 v v v e e e
欧拉定理:( v + 1 ) − e + N = 2 (v+1)-e+N=2 ( v + 1 ) − e + N = 2
注意一个顶点至少和三条边关联,所以 3 ( v + 1 ) ≤ 2 e 3(v+1) \le 2e 3 ( v + 1 ) ≤ 2 e
由以上两个式子即可推出 v ≤ 2 N − 5 v \le 2N-5 v ≤ 2 N − 5 e ≤ 3 N − 6 e \le 3N-6 e ≤ 3 N − 6
知道了 V 图的点数和边数都是 O ( N ) O(N) O ( N )
O ( N ) O(N) O ( N ) N N N O ( N ) O(N) O ( N ) N N N
所以问题的关键是:我们如何高效地建出 N N N s i s_i s i O ( N log N ) O(N \log N) O ( N log N )
下面我们来看一个经典的 Art Gallery Problems :(凹)多边形内最少布置多少守卫才能看到所有位置。
注意这个问题已被证明是 NP-Hard 的,所以我们尝试求一些紧的界。首先一个显然的上界是 N − 2 N-2 N − 2 N N N N − 2 N-2 N − 2
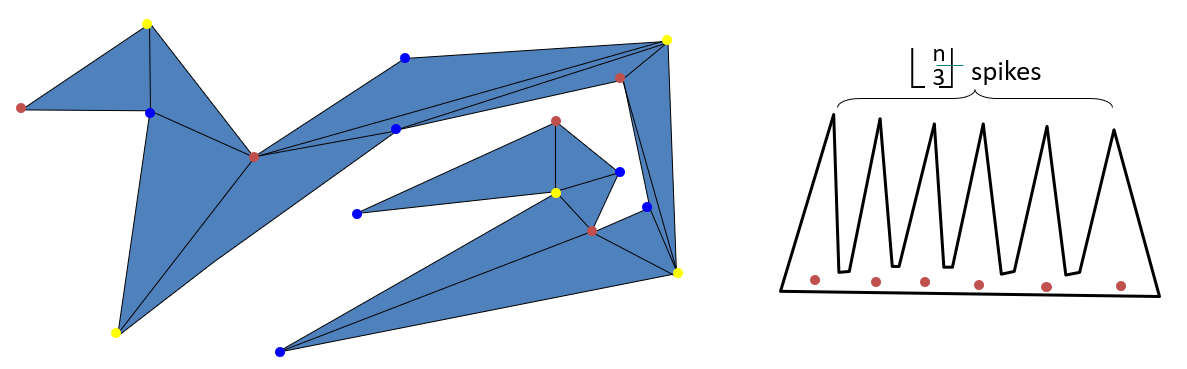
N = 3 N=3 N = 3 1 1 1 N > 3 N>3 N > 3 u u u v , w v,w v , w ( v , w ) (v,w) ( v , w ) ( u , v , w ) (u,v,w) ( u , v , w ) u u u u ′ u' u ′ ( u , u ′ ) (u,u') ( u , u ′ )
现在我们再来证明一个更紧的上界。如果把多边形(任意一个)三角形剖分后的边也连上去,我们可以用对偶证明,新图的顶点是可以三染色的。更厉害的是,如果我们在三染色的任意一种颜色处放置守卫,均能覆盖整个多边形!那么挑一种出现次数最少的颜色,我们可以得到 Art Gallery Problems 的上界:⌊ N 3 ⌋ \lfloor \frac{N}{3} \rfloor ⌊ 3 N ⌋
事实上我们还能构造出达到这一上界的多边形,见右图。