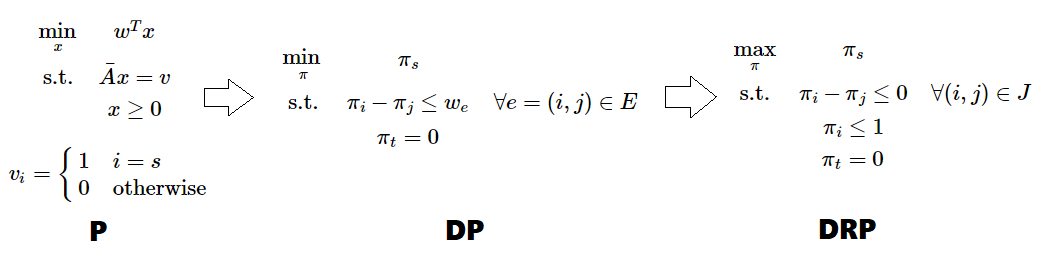• 我在大三春夏学期上了张国川老师的《应用运筹学基础》这门课。
  • 张国川老师坚持板书讲解，课上干货满满，是不可多得的好老师。
  • 我本来是在 TSR 学长的博客 的基础上补充知识点的。张老师在期末时把“上课笔记整理”也作为了考核方式之一，于是我把 TSR 学长的部分内容也结合进来了。
  • 这篇文章是系列之二，还有两个系列分别是：

原始对偶方法

  • 基本思想：

    • 灵活运用了互补松弛条件 (y∗TA−cT)x∗=0(y^{\ast {\rm T}}A-c^{\rm T})x^\ast=0 且 y∗T(Ax∗−b)=0y^{\ast {\rm T}}(Ax^\ast-b) = 0.
    • 给出一组对偶的解，强行去满足互补松弛条件。每次观察 xx 是否满足原问题的约束，若不满足就不断地修正 yy。

  • 原始对偶算法 流程

    1. 我们先列出原问题（P）的对偶问题（DP），并找到 yy 的一组可行解。
      • 如果 c≥0c \ge 0，直接取 y=0y=\pmb{0} 即可。
      • 否则我们给原问题增加一个变量与一条约束 x1+x2+⋯+xn+xn+1=bm+1x_1 + x_2 + \dots + x_n + x_{n+1} = b_{m+1}，其中 bm+1b_{m+1} 需要足够大，至少要大等于 x1+x2+⋯+xnx_1 + x_2 + \dots + x_n 可能的最大值。
      • 加入新约束后，对偶问题的约束变成了 ATy+ym+1[1,1,…,1]T≤cA^Ty + y_{m+1}\begin{bmatrix} 1,1,\dots,1 \end{bmatrix}^T \le c，目标函数变成了 max⁡bTy+bm+1ym+1,ym+1≤0\max b^Ty + b_{m+1}y_{m+1}, y_{m+1} \le 0。取可行解 yi(i∈[1..m])=0,ym+1=min⁡ciy_i(i \in [1..m])=0,y_{m+1}=\min c_i
    2. 现在我们需要寻找一个原问题的可行解 xx 满足互补松弛定理。设 AjA_j 表示矩阵 AA 的第 jj 列，定义 J={j∣AjTy=cj}J = \{ j | A_j^Ty = c_j \}。根据原问题的定义和互补松弛定理，我们想要找到符合要求的 xx 使得 xj=0,∀j∉Jx_j = 0,\forall j \not\in J 且 xj≥0,∀j∈Jx_j \ge 0,\forall j \in J 。
    3. 构造一个带限制的原问题（RP）。如果 RP 的目标值取 00，我们就找到了符合要求的 xx。
    4. 再构造 RP 的对偶问题（DRP），设 yˉ\bar{y} 是DRP的最优解。显然 yˉ=0\bar{y}=\pmb{0} 是一组可行解，若其也是最优解，则当前对偶可行的 yy 就是对偶问题的最优解。
    5. 若 yy 目前不是最优解，则 yˉ>0\bar{y}>\pmb{0} ，我们想办法用 yˉ\bar{y} 改进 yy：设 y^=y+θyˉ\hat{y} = y + \theta\bar{y}（其中 θ≥0\theta \ge 0）。注意到，y^\hat{y} 仍然需要是对偶可行的，即 ATy^=ATy+θATy^≤cA^T\hat{y} = A^Ty + \theta A^T\hat{y} \le c 仍要满足。
    6. 考虑 θ\theta 的取值范围。对于 j∈Jj \in J，因为 AjTyˉ≤0A^T_j\bar{y} \le 0，无论 θ\theta 取多大，都不会超过 cc 的限制，所以这些项不会限制 θ\theta 的取值；对于 j∉Jj \not\in J，我们选择 θ=min⁡j∉J,AjTyˉ>0cj−AjTyAjTyˉ\theta = \min_{j \not\in J, A^T_j\bar{y} > 0} \frac{c_j - A^T_jy}{A^T_j\bar{y}} 。这样就能让 j∉Jj \not\in J 中的一条限制变紧，且其它限制则不会超过。
    7. 将 yy 调整为 y^\hat{y} 之后，进入下一轮迭代调整，直到 DRP 的最优解让目标函数值为 0

  • 经典例子：最短路问题

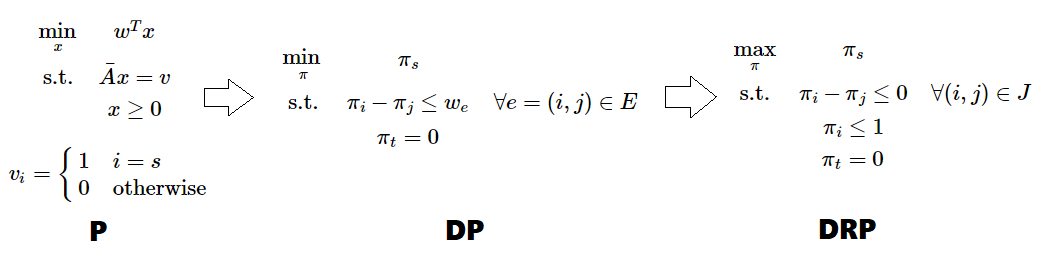
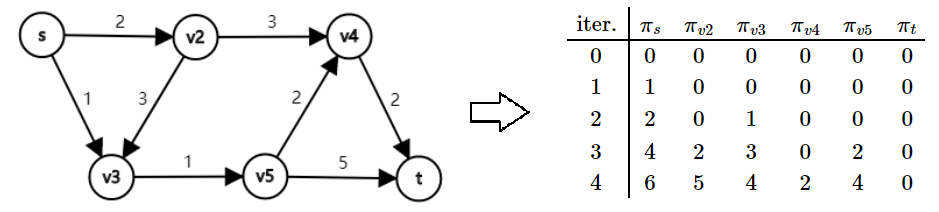
    1. 我们用图的点 - 弧关联矩阵表示 ss 到 tt 的线性规划问题。因为矩阵 AA 是全幺模矩阵，解出的实数最优解必然是整数解。下面我们尝试用原始对偶方法解这个线性规划。
    2. AA 矩阵显然是线性相关的（把 AA 的每一行加起来得到零向量）不妨从 AA 中去掉代表终点 tt 的那一行，得到新矩阵 Aˉ\bar A。即新的线性规划是原问题（P）。
    3. 我们写出对偶问题（DP）（它其实就是差分约束系统）和带限制的对偶问题（DRP）。
    4. 这个 DRP 非常得清晰。如果想要让 πs\pi_s 取成 00，必须保证 tt 也在和 ss 相关的连通块（右πi−πj=we\pi_i-\pi_j=w_e 的 ee 组成的连通块）里。所以我们不断更新 π\pi ，每次把 JJ 里的点的 πi\pi_i 集体提升到尽可能的大。每次提升 JJ 里的元素单调增加，复杂度为 O(NM)O(NM)。

  • 对偶问题 DP 优化的函数值就是最短路的直接证明（作业题）

  1. 找到 ss 到 tt 的任意一条最短路。向量 f\pmb{f} 满足：fi\pmb{f}_i 是这条最短路从 ss 到 ii 经过的边的权值和，同时记 F=ftF=\pmb{f}_t.
  2. 设向量 g\pmb{g} 是该对偶问题取到最大值时的一组解，记 GG 为最大值。
  3. 因为 f\pmb{f} 表示一条最短路，由最短路性质，我们发现 f\pmb{f} 是满足上述线性规划限制的一组可行解。由 g\pmb{g} 是一组最优解，所以 F≤GF \le G.
  4. 现在只需证明 F≥GF \ge G 即可说明 F=GF=G。反证，假设 F<GF < G.
  5. 由 fs≥gs=0,ft<gt\pmb{f}_s \ge \pmb{g}_s=0,\pmb{f}_t < \pmb{g}_t，f\pmb{f} 表示的最短路径上必然存在一条边 e=(u→v,w)e=(u \rightarrow v,w)，满足 fu≥gu, fv<gv\pmb{f}_u \ge \pmb{g}_u,~\pmb{f}_v < \pmb{g}_v. 所以 fv−fu<gv−gu\pmb{f}_v-\pmb{f}_u < \pmb{g}_v - \pmb{g}_u. 因为 f\pmb{f} 表示最短路径，所以 fv−fu=w\pmb{f}_v-\pmb{f}_u=w，即 gv−gu>w\pmb{g}_v-\pmb{g}_u>w，这和 g\pmb{g} 是该线性规划的一组可行解矛盾。所以假设不成立，即 F≥GF \ge G。
  6. 最终我们得到 F=GF=G，原命题得证。

整数线性规划

  • TSP 问题

    • 考虑如何用线性规划表示
      • min⁡∑e=(i,j)ci,jxi,j\min{\sum \limits_{e=(i,j)} c_{i,j}x_{i,j}}
      • 其中 xi,j∈{0,1}x_{i,j} \in \{0,1\}，xi,j=1x_{i,j}=1 当且仅当 (i,j)(i,j) 是环上的相邻两点。
    • 尝试更形式化地表达
      • 构成环的必要条件：∀i∑j=1nxi,j=1\forall i\sum \limits_{j=1}^n x_{i,j}=1 且 ∀j∑i=1nxi,j=1\forall j \sum \limits_{i=1}^n x_{i,j}=1。
      • 若只有这两个限制，会导致多个不相交圈的情况：要强制让所有点都与 11 号点同圈。
      • 因此，新增 u1,…,unu1,\dots,u_n 这 nn 个辅助变量并加一个新约束：ui−uj+nxi,j≤n−1u_i - u_j + n x_{i,j} \le n-1，其中 1≤i≤n,2≤j≤n,i≠j1 \le i \le n, 2 \le j \le n, i \ne j.
    • 证明以上约束的正确性
      • 对于一个多圈的解，必然存在一个圈不包含 11。沿圈上走一圈，上述限制 xi,jx_{i,j} 都会取 11。将这些不等式全部加起来，会得到 kn≤k(n−1)kn \le k(n-1)（kk 是圈的长度），产生矛盾。说明必然有约束不能满足。
      • 对于一个单圈的解，一种 uiu_i 的可行取法是：u1=0,up2=1,up3=2,…,upn−1=n−1u_1=0,u_{p_2}=1,u_{p_3}=2,\dots,u_{p_{n-1}}=n-1，其中 pip_i 表示TSP问题里从 11 出发顺次访问到的第 ii 个点。对比上一条，约束能满足的原因是：jj 是从 22 开始取的，upn−1u_{p_{n-1}} 到 u1=1u_1=1 是没有限制的。
      • 对于不在圈上的边，xi,j=0x_{i,j}=0，即 ui−uj≤n−1u_i-u_j \le n-1。审视上一条，最大的 uiu_i 也是 n−1n-1，所以可行。
      • uiu_i 就像是每个点在环上的“势”，可以集体地增减。我认为只要限制 ui≥0u_i \ge 0 就能正确地求出一组解（无需 uiu_i 是整数的限制，因为也可以 uiu_i 全体是实数）。如果加一条适当的限制（如 ∑ui=n×(n−1)2\sum u_i = \frac{n\times(n-1)}{2}），跑出来的最优解必然是整数。

  • 01 背包

    • 线性规划模型
      • max⁡∑i=1nvixi\max \limits \sum_{i=1}^{n} v_{i} x_{i}
      •  s.t. xi∈{0,1},∑i=1nwixi≤C\text { s.t. } x_{i} \in\{0,1\},\sum_{i=1}^{n} w_{i} x_{i} \leq C
    • 贪心解及其近似度分析
      • 朴素贪心做法：将物品按 viwi\frac{v_i}{w_i} 从大到小排序，依次塞入背包直到装不下。
      • 该算法近似比是无穷大，分析如下：
        • 我们求上述线性规划的实数解，记为 LP(I)\mathrm{LP(I)}。
        • 观察 LP(I)\mathrm{LP(I)} 解的结构：性价比前 mm 大的物品一定是完整地取走，剩下的某一个物品取了“分数”个（可以用调整法证明）。不妨设前 mm 个物品的总价值是 α\alpha，剩下取的那个物品价值是 β\beta，我们可以得到 OPT(I)≤LP(I)≤α+β,Greedy(I)≥α\mathrm{OPT(I) \le LP(I) \le \alpha + \beta, Greedy(I) \ge \alpha}
        • 基于以上分析，贪心解近似比 =OPT(I)Greedy(I)≤α+βα=1+βα=\mathrm{\frac{OPT(I)}{Greedy(I)}} \le \frac{\alpha+\beta}{\alpha} = 1 + \frac{\beta}{\alpha}
        • 若前 mm 个物品体积和是 2ϵ2 \epsilon、单位价值是 v0v_0，剩下选的物品是 C−ϵC-\epsilon、v02\frac{v_0}{2}，则 βα=C−ϵ4ϵ→+∞\frac{\beta}{\alpha} = \frac{C-\epsilon}{4\epsilon} \rightarrow +\infty
      • Trick：我们修改一下上述贪心做法：当 α<β\alpha < \beta 时我们只取后者。这样 Greedy(I)≥max⁡(α,β)\mathrm{Greedy(I) \ge \max(\alpha, \beta)}，近似比为 =OPT(I)Greedy(I)≤max⁡(α,β)α≤2=\mathrm{\frac{OPT(I)}{Greedy(I)}} \le \frac{\max(\alpha, \beta)}{\alpha} \le 2，即近似比为 22.
    • 近似做法
      • 朴素反向背包算法：设 fj,if_{j,i} 表示前 jj 个物品中，选的价值总和恰好是 ii，最少需要的空间。直接做的复杂度是 O(n2Vmax)O(n^2V_{max})，能得到最优解。
      • 现在对价值进行 Scaling：把每个物品的价值调整成 ⌊Vik⌋\lfloor \frac{V_i}{k} \rfloor后再DP，kk 是某个常数。
    • 下面证明：该 Scaling 做法是完全多项式算法。
      • 完全多项式算法：既是读入规模的多项式，也是近似比ϵ\epsilon 的多项式。
      • 设原问题最优集合是 SS，答案是 OO；小规模问题最优集合是 S′S'，答案是 O′O'.
      • O′=∑j∈S′Vj′≥k∑j∈S′Vj≥∑j∈S(Vjk−1)≥O−nkO'=\sum \limits_{j \in S'} V_{j}^{'} \ge k \sum \limits_{j \in S'}V_j \ge \sum \limits_{j \in S} (\frac{V_j}{k}-1) \ge O-nk
      • 令 k=ϵnVmaxk = \frac{\epsilon}{n}V_{max}，则 O′≥(1−ϵ)OO' \ge (1-\epsilon) O，且复杂度是 O(n3ϵ)O(\frac{n^3}{\epsilon})

  • 匹配问题

    • 设图的点集为 VV，边集为 EE， (i,j)∈E(i, j) \in E 表示从第 ii 个点连到第 jj 个点的一条有向边，xi,jx_{i, j} 表示这条边是否为匹配边。那么一般无向图的最大匹配问题可以写成：
      • max⁡∑(i,j)∈Exi,j\max \sum\limits_{(i, j) \in E} x_{i, j}
      • s.t.∑(i,j)∈Exi,j≤1∀i∈V\text{s.t.} \quad \sum\limits_{(i, j) \in E} x_{i, j} \le 1 \quad \forall i \in V 且 ∑(i,j)∈Exi,j≤1∀j∈V\sum\limits_{(i, j) \in E} x_{i, j} \le 1 \quad \forall j \in V
      • 其中 xi,j∈{0,1}x_{i, j} \in \{0, 1\}。
    • 我们也可以用图的点 - 边关联矩阵来描述匹配问题。设图中有 nn 个顶点，mm 条边，那么图的点 - 边关联矩阵是一个 n×mn \times m 的矩阵。该矩阵每列对应一条边，每行对应一个顶点。若第 ii 个顶点是第 jj 条边的端点，那么矩阵第 ii 行第 jj 列为 1，否则为 0（可以看出，这个矩阵描绘的是无向边）。这样，一般无向图的最大匹配问题写为：
      • max⁡(i,j)∈E∑xi,j\max\limits_{(i, j) \in E} \sum x_{i, j}
      • s.t.Ax≤b\text{s.t.} \quad Ax \le b，其中 xi,j∈{0,1}x_{i, j} \in \{0, 1\}.
    • 注意，用线性规划求解二分图的最大匹配问题，最优解的 xix_i 取值非 0 即 1。因为可以证明（数学归纳法），二分图的点-边关联矩阵是全幺模矩阵。
    • 二分图最大匹配的对偶问题是二分图的最小点覆盖。

  • Gomory 割平面法

    • 基本思想：不断增加限制平面，直到某一次求得的最优解为整数。
    • 若我们用单纯形法求解后获得的不全是整数解，选择一个非整数的变量 xix_i，其必然满足：
      xi+∑j=m+1nai,jˉxj=biˉ①x_i + \sum\limits_{j=m+1}^n \bar{a_{i,j}}x_j = \bar{b_i} \quad \text{①}
    • 既然 xix_i 不是整数且 xm+1∼n=0x_{m+1 \sim n} = \pmb{0}，说明 biˉ\bar{b_i} 一定不是整数，则加入以下限制不会影响原来的整数解空间：
      xi+∑j=m+1n⌊ai,jˉ⌋xj≤⌊biˉ⌋②x_i + \sum\limits_{j=m+1}^n \left\lfloor \bar{a_{i,j}} \right\rfloor x_j \le \left\lfloor\bar{b_i}\right\rfloor \quad \text{②}
      • 现在我们就多了②这个限制，把它加进约束里进一步求解即可。一般我们会加入①-②，这样限制更简单些：
        ∑j=m+1n(ai,jˉ−⌊ai,jˉ⌋)xj≥biˉ−⌊biˉ⌋①−②\sum\limits_{j=m+1}^n(\bar{a_{i,j}} - \left\lfloor \bar{a_{i,j}} \right\rfloor) x_j \ge \bar{b_i} - \left\lfloor \bar{b_i} \right\rfloor \quad \text{①}-\text{②}

  • 分枝定界法

    • 分枝定界法的思想和最优性剪枝或者 min-max 搜索树类似。
    • 我们先解实数线性规划，得到了整数规划最优解的上界。假设最优解中 xi(k<xi<k+1)x_i(k < x_i < k+1) 不是整数，就会有两种可能：xi≤kx_i \le k 或 xi≥k+1x_i \ge k+1，对两种情况分别进行搜索。
    • 如果在某一枝内算出了一个整数解，我们就得到了原整数规划最优解的下界。
    • 某个搜索分支结束有三种可能：
      • 当前线性规划无可行解（死枝）。
      • 当前（实数）最优解未超过下界（枯枝）。
      • 当前已经是整数解（活枝）。

基于线性规划的近似算法

  • 带权点覆盖问题的LP解法

    • 设 xix_i 表示第 ii 个点是否选，我们可以列出一个整数线性规划问题；每条边 (u,v)(u,v) 即为一个限制 xu+xv≥1x_u+x_v \ge 1，目标函数即为 W=∑vixiW=\sum v_i x_i.
    • 将这个线性规划一般化: 0≤xi≤10 \le x_i \le 1。这样能在多项式内求出一个最优解 W∗W^*，其优于原来的最优解。
    • 现在我们把 W∗W^* 对应的 x\pmb{x} 做这样的改动：xi′=[xi]x'_i=[x_i]（四舍五入）。
    • 显然，x′\pmb{x'} 也是符合该线性规划的一组解（对于任意一组限制，至少存在一个 xi≥0.5x_i \ge 0.5；这时候对应的 xi′x'_i 取成 11，满足限制要求）
    • 然后，每一个取 11 的 xi′x'_i 增幅最多只有 0.50.5，即新的 W′W' 满足 W′≤2W∗W' \le 2W^\ast。
    • 所以该做法的近似度是 22。

  • 带权点覆盖问题的对偶解法

    • 接下来这种 2-近似做法只需用到原始对偶的思想，可以避开线性规划求解。
    • 原问题的对偶问题是：求 max⁡e∈Eye\max \limits_{e \in E} y_e，使得对于所有的 i∈Vi \in V，∑i∈eye≥wi\sum \limits_{i \in e} y_e \ge w_i 且 ye≥0y_e \ge 0.
    • 列出互补松弛条件
      • PCS: xi(∑e∈Eye−we)=0x_i(\sum \limits_{e \in E} y_e-w_e)=0
      • DCS: ye(xi+xj−1)=0y_e(x_i+x_j-1)=0 其中 e=(i,j)e=(i,j)
    • 在整数线性规划上考虑一个弱化后的互补松弛条件：
      • PCS成立：xi=0x_i = 0 或 xi≠0x_i \ne 0 且 wi=∑i∈eyew_i = \sum \limits_{i \in e} y_e
      • DCS不太差：ye=0y_e = 0 或 ye≠0y_e \ne 0 且 1≤xi+xj≤21 \le x_i + x_j \le 2
    • 首先我们证明：若该条件成立，近似比为 22（x∗x^{\ast} 表示原问题的最优解）。
      • ∑i=1n(∑i∈eye)xi=∑e∈Eye(xi+xj)≤2∑e∈Eye≤2∑i=1nwixi∗≤2OPT\sum \limits_{i=1}^n (\sum \limits_{i \in e} y_e)x_i = \sum \limits_{e \in E} y_e(x_i+x_j) \le 2\sum \limits_{e \in E}y_e \le 2\sum \limits_{i=1}^n w_ix^{\ast}_i \le 2\mathrm{OPT}
    • 算法
      1. 初始设 x=0,y=0\pmb{x}=0, \pmb{y}=0，所有边未标记。此时 x\pmb{x} 不可行但是 y\pmb{y} 可行。
      2. 任选一条未标记的边 ee，增加 yey_e 的值直到某一端点 ii 约束变紧。
      3. 设 xi=1x_i=1，将 ii 放入顶点覆盖集，并把与 ii 相关的边都标记。
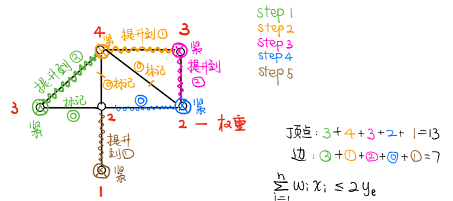
      4. 重复以上两步直到所有边都被标记。
    • 引用 MCL 大佬的图

  • Unrelated Parallel Machine Scheduling 问题

    • tsr 的 UPMS问题讲解
    • 有 mm 台机器和 nn 件物品，每件物品都要在一台机器上加工，第 ii 台机器加工第 jj 件物品的时间为 ai,ja_{i, j}。求一种把物品分配给机器的方案，使得加工总时长最长的机器加工时间最短。
    • 优化模型很简单：
      • min⁡x,tt\min\limits_{x, t} t
      • s.t.∑i=1mxi,j=1∀j∈{1,2,…,n}\text{s.t.} \quad \sum\limits_{i=1}^m x_{i, j} = 1 \quad \forall j \in \{1, 2, \dots, n\}
        ∑j=1nai,jxi,j≤t∀i∈{1,2,…,m}\qquad \sum\limits_{j=1}^n a_{i, j}x_{i, j} \le t \quad \forall i \in \{1, 2, \dots, m\}
      • xi,j∈{0,1}x_{i, j} \in \{0, 1\}
    • 注意到 tt 有二分性。现在我们二分 tt，每次直接解实数线性规划来判是否存在可行解。设最终稳定的值是 TT，对应的实数解是 x∗x^\ast。显然 TT 是答案的一个下界，即 T≤OPTT \le \text{OPT}.
      • 对于第 jj 件物品，若 ∃i xi,j∗=1\exists i ~ x^\ast_{i, j} = 1 那么称该物品为“整数物品”，否则称为“分数物品”。设共有 n1n_1 个“整数物品”，n2n_2 个“分数物品”，显然有 n1+n2=nn_1 + n_2 = n
      • 若第 jj 件物品为“分数物品”，那么 xi,jx_{i, j} 中至少有两个非零值。原问题有 n+mn+m 条限制，根据单纯形法，非零的变量至多有 n+mn+m 个，那么 n1+2n2≤n+mn_1 + 2n_2 \le n + m，得到 n2≤mn_2 \le m。
    • 下面我们给每台机器分配物品，使得每台机器的加工总时长都不超过 2T2T，以此说明近似比是 22。
      • 先做一个小处理：把用时大于 TT 的物品都移除（显然是等价的）。
      • 构造一张二分图：左边有 mm 个点，每个点表示一台机器；右边有 nn 个点，每个点表示一件物品。若 xi,j>0x_{i, j} > 0 则连接第 ii 台机器和第 jj 件物品。
      • 一个重要的性质：该二分图边数不超过点数。
      • 首先考虑“整数物品”。很显然，每个“整数物品” jj 都只和一台机器 ii 有连边 (i,j)(i, j)，那就把“整数物品” jj 放在机器 ii 中加工，并去掉物品 jj 和边 (i,j)(i, j)。由于每次恰好去除一个点和一条边，性质依然成立。
      • 这样，图中就只剩机器和“分数物品”了。考虑所有度数为 11 的机器 ii。假设唯一连接机器 ii 的边是 (i,j)(i, j)，那么我们把“分数物品” jj 放在机器 ii 中加工，并去掉机器 ii、物品 jj 和物品 jj 的所有连边。由于每件“分数物品”都有至少两条连边（度数至少为 2），所以我们每次都会去掉两个点以及至少两条边，性质依然成立。
      • 反复操作直到最后不存在度数为 11 的机器为止，剩下的图一定是由若干个偶环构成。所以从始至终，我们总能通过合理分配，使得每台机器至多分配到一个“分数物品”。每台机器在完成原来若干整数任务的同时，独立地把分配给自己的那个“分数物品”做完。注意一件物品的加工时间至多为 TT，所以现在的用时最多是 2T2T。