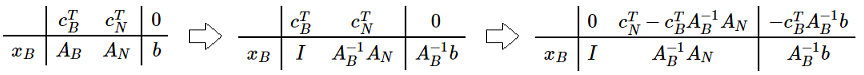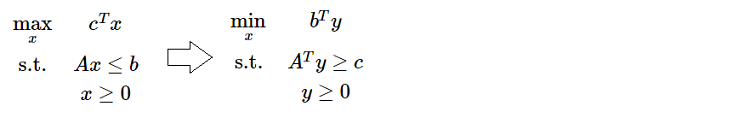应用运筹学-线性规划的基本理论

• 我在大三春夏学期上了张国川老师的《应用运筹学基础》这门课。
• 张国川老师坚持板书讲解，课上干货满满，是不可多得的好老师。
• 我本来是在 TSR 学长的博客 的基础上补充知识点的。张老师在期末时把“上课笔记整理”也作为了考核方式之一，于是我把 TSR 学长的部分内容也结合进来了。
• 这篇文章是系列之一，还有两个系列分别是：
  • 线性规划应用
  • 近似算法选讲

凸集、凸函数、凸优化

• 凸集：任取 $x, y \in S$ 和 $\forall \theta \in [0,1]$ 满足 $\theta x + (1-\theta)y \in S$，称集合 $S$ 凸集（Convex Set）。
  • 凸集的交仍然是凸集。
  • 如果没有 $\forall \theta \in [0,1]$ 的条件，称集合 $S$ 仿射集（Affine set）。
• 凸函数：对于定义在凸集 $S$ 上的函数 $f(x)$，若对于 $\forall \theta \in [0,1]$ 有 $f(\theta x + (1-\theta) y) \le \theta f(x) + (1-\theta) f(y)$，那么称 $f(x)$ 是凸函数（Convex Function）。
  • 延森不等式（Jensen’s inequality）：若 $f(x)$ 是凸函数， $f(\sum_{i=1}^n \theta_ix_i) \le \sum_{i=1}^n \theta_i f(x_i)$
  • 定理：凸函数的局部最优就是全局最优。
    1. 假设 $\hat{x}$ 是局部最优点，$x^\ast$ 为全局最优点，则 $f(\hat{x}) > f(x^\ast)$。
    2. 由于 $f(x)$ 为凸函数，那么对于点 $x = \theta \hat{x} + (1-\theta)x^\ast$ 有 $f(x) \le \theta f(\hat{x}) + (1-\theta) f(x^\ast) < f(\hat{x})$。
    3. 取 $\theta = 1 - \frac{\epsilon}{2|\hat{x}-x^\ast|}$，就有 $|x - \hat{x}| = \frac{\epsilon}{2} < \epsilon$，说明 $x$ 在 $\hat{x}$ 的邻域内且比它优，矛盾。
  • 凸函数的判定条件：
    • 一阶判定条件：设 $f(x)$ 在凸集 $C$ 上一阶可微，则该函数为凸的充要条件是：对于 $\forall x, y \in C$，都满足 $f(y) \ge f(x) + \nabla f(x)^T(y-x)$.
    • 二阶判定条件：设 $f(x)$ 在凸集 $C$ 上二阶可微，则该函数为凸的充要条件是：对 $\forall x \in C$，都满足 $\nabla^2(x) \succeq 0$。
• 凸优化：优化 $\min f(x) \quad \text{s.t. } g_{i}(x) \leq 0,i \in [1..m] \quad h_{i}(x)=0, i \in [1..p]$。其中 $f(x),g_i(x)$ 是凸函数，$h_i(x)$ 是仿射函数。
  • 定义拉格朗日函数 $L$：$ \mathbf{R}^{n} \times \mathbf{R}^{m} \times \mathbf{R}^{p} \mapsto \mathbf{R}$, $ L(x, \lambda, v)=f{0}(x)+\sum_{i=1}^{m} \lambda_{i} g_{i}(x)+\sum_{i=1}^{p} v_{i} h_{i}(x)$
  • 最优解 $\pmb{(x,\lambda,v)}$ 满足 KKT 条件
    • 原始条件：$g_i(x) \le 0, h_i(x) =0$
    • 拉格朗日函数梯度为 $0$：$\nabla_x L = \pmb{0}$
    • 对偶约束：$\lambda_i \ge 0$
    • 互补松弛条件：$\lambda_ig_i(x)=0$

线性规划的定义

• 左边形式的问题被称为线性规划（Linear Programming）
  
  • 由于仿射函数既是凸函数又是凹函数，所以优化问题是 min 还是 max 问题不大；常数 $d$ 对优化问题的解没有影响，一般也可以去掉。这就变成了中间的这个优化函数。
  • 对于 $Ax \le b$ 这个约束，可以通过添加非负变量将其松弛成等式。所以我们总能将线性规划转成右侧的形式。右式也称为线性规划的典则形式。
• 极点：若 $x \in S$ 无法表示为凸集 $S$ 内某两个元素的凸组合，称 $x$ 是极点（extreme point）。
  • LP 问题的可行域实际上是很多超平面的交，最后组成的应该是一个超多面体。
  • 极点就是超多面体的“顶点”。可以证明，若最优解有解，必然取在极点上：
    1. 假设最优点 $O$ 严格在凸集里面。任取一条与凸集交在 $P$ 和 $Q$ 的直线。因为是线性规划问题，$O$ 点处的函数值一定是 $P$ 点和 $Q$ 点的线性组合。所以 $P$ 和 $Q$ 中，至少有一处的函数值是大于等于 $O$ 的。
    2. 我们可以重复上述步骤，把最优点一步一步约束到顶点上。比如在三维中，我们先将其“规约”到凸壳的表面上，最后“规约”到凸壳的边和点上。
• 基可行解：我们讨论 $Ax = b$ 有解且行满秩的情况（如果不满秩就去掉线性相关的限制条件）。设 $A$ 是一个 $m \times n$ 的矩阵，根据线性代数的知识，我们可以从 $A$ 中选出最多 $m$ 列线性无关的列向量，其它列向量都和它们线性相关。我们把这 $m$ 个列向量调整到前面去，把 $A$ 分成两部分：$A = \begin{bmatrix} A_B & A_N \end{bmatrix}$.容易构造出 $Ax = b$ 的一个解：$x = \begin{bmatrix} A_B^{-1}b \quad 0 \end{bmatrix}^T$，称这种解为基可行解（Basic Feasible Solution）。显然，基可行解至多有 $C_n^m$ 种。
  • 定理1：每个极点都对应着一个基可行解，且每个基可行解都对应着一个极点。
  • 定理2：最优解一定可以在基可行解处取到。
• tsr 的概念讲解

单纯形法

• 单纯形法（Simplex Method）（以 $\max$ 模型为例）
  1. 将 $A$ 中的基变量消成单位矩阵，并把目标函数基变量的系数都消成 $0$。
  2. 以某种策略找一个 $c_j>0$ 的非基变量 $j$ 入基。
  3. 依次考察 $b_i > 0$ 的行，确定一行 $i$ 使得 $\frac{b_i}{A_{i,j}}$ 最小（对于 $j$ 最紧的限制）。
  4. 拿第 $i$ 行去消，把每一行的 $A_{?,j}$ 以及目标函数的 $c_j$ 都消成 $0$。即第 $i$ 行的基变量出基。
  5. 重复步骤 $2 \sim 4$ 直到检验数全大于 $0$.
• 单纯形表（Simplex Tabuleau）
  • 变量分成基变量和非基变量：设 $c^T = \begin{bmatrix} c_B^T & c_N^T \end{bmatrix}$， $A = \begin{bmatrix} A_B & A_N \end{bmatrix}$，$x = \begin{bmatrix} x_B^T & x_N^T \end{bmatrix}^T$
  • 显然我们有 $A_Bx_B + A_Nx_N = b$ 且 $z = c_B^Tx_B + c_N^Tx_N$
  • 通过简单的线性变换有：
    
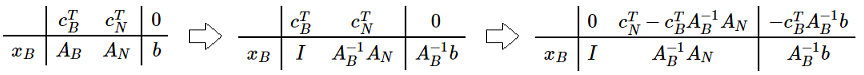
  • 这其实就是单纯形法的形式化迭代过程
• 评价
  • 变换的本质是：在满足约束的限制下，用不同的非基变量组合来表示目标函数。
  • 当非基变量的检验值均 $\le 0$ 时取到最大值。我们可以想象成，目标函数就是由这些非基变量决定的，它们目前都取了 $0$，而且任意变量的微小增长都会导致结果变劣。
  • 单纯形正确性证明
    1. 设最终的检验数是 $\hat{c}$（均小于 $0$），对应的解是 $x$，最优解是 $y$。
    2. 令 $d=x-y$，我们有 $Ax - Ay = b - b = 0 = Ad = A_Bd_B + A_Nd_N$
    3. 那么 $d_B = -A_B^{-1}A_Nd_N$，则 $c^Td = c_B^Td_B + c_N^Td_N = (c_N^T-c_B^TA_B^{-1}A_N)d_N = \hat{c}d_N$
    4. 我们知道 $x_N = 0$，又 $y \ge 0$，所以 $d_N \ge 0$；又 $\hat{c} \le 0$，所以 $c^Td = \hat{c}d_N \le 0$，那么 $c^Ty = c^Tx + c^Td \le c^Tx$，说明 $y$ 并没有比 $x$ 更优。
  • 在非退化情况下，单纯形法一定可以停止。因为每次迭代都会让答案更优一点，访问的基可行解空间是不会重复的。而基可行解数量又是有限的，所以算法一定可以停止。
  • 可以证明，如果按字典序的顺序选取 $j$，单纯形算法一定可以停止。
• tsr 讲解单纯形法

单纯形法的初始可行解

• 初始可行解
  • 若单纯形的约束是 $Ax \leq b$，初始可行解可以取 $x = \pmb{0}$.
  • 若约束是 $Ax = b$ 时，我们可以通过加入松弛变量 $\bar{x}$ 使得 $Ax + \bar{x} = b$，这样 $x = \pmb{0}, \bar{x} = b$ 是初始可行解。这里存在一个问题：$\bar{x}$ 是我们添加进去的变量——我们希望 $\bar{x}$ 能全部出基。
• 大 M 法（Big M Method）
  • 对不为 $0$ 的 $\bar{x}$ 进行“惩罚”。将目标函数改为 $z = c^Tx - M\sum_{i=1}^m\bar{x}_i$。如果 $M$ 是一个足够大的正数，$\bar{x}$ 就会在 $-M$ 这个“严厉的惩罚”之下变成 $0$。
  • $M$ 取多大很难说，且取得过大会影响精度。
• 两阶段法（Two-Phase Method）
  • 添加了 $\bar{x}$ 后，我们考虑一个新的线性规划：约束不变，改成优化 $\min {\sum \bar{x}_i}$ 这个函数。一组显然的初始可行解是 $x = \pmb{0}, \bar{x} = b$.
  • 如果这个优化问题的最优解的目标函数值不为 $0$，则原问题无可行解；否则我们就找到了原问题的一组可行解。我们再以这个可行解为起点，利用单纯形法求出原问题的最优解即可。
  • 由此可以发现，线性规划的可行解和最优解求解难度相同。
• 思考：对于 $\max c^Tx,Ax \le b$ 这个模型，如果突然多了一个 $x_1 \ge 4$ 的条件怎么办？
  • 添加一个松弛变量 $\overline{x}$： $-x_1+\overline{x} = -4$
  • 此时会发生一个问题：$\overline{x}$ 和 $b$ 至少有一个会取负号，不符合约束。
  • 怎么办呢？再引进一个变量 $\hat{x}$：$x_1-\overline{x}+\hat{x}=4$
  • 至此，$\hat{x}=4$ 是新问题的一个可行解，直接套大M法或二阶段法求解。
• tsr 讲解初始可行解

对偶定理与对偶单纯形法

• 线性规划的对偶
  
  
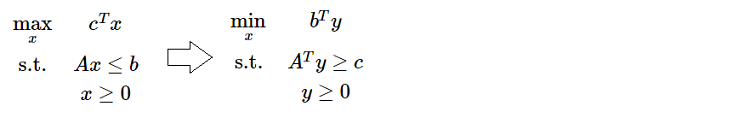
• 对偶定理
  • 弱对偶定理 (Weak Duality)：设 $x$ 和 $y$ 分别是原问题和对偶问题的可行解，则 $c^{\rm T}x \le b^{\rm T}y$。证明：由 $y$ 的可行性我们有 $A^{\rm T}y \ge c$，即 $y^{\rm T}A \ge c^{\rm T}$，两边同乘以 $x$ 有 $y^{\rm T}Ax \ge c^{\rm T}x$；由 $x$ 的可行性还有 $Ax \le b$，那么 $y^{\rm T}Ax \le y^{\rm T}b$，合起来就是 $c^{\rm T}x \le b^{\rm T}y$。
    • 最优性：若 $x$ 和 $y$ 分别是原问题和对偶问题的可行解，而且 $c^\mathrm{T}x=b^\mathrm{T}y$，那么 $x$ 和 $y$ 分别是原问题和对偶问题的最优解。
    • 可行性：若原问题无最优解（可以取无穷大），则对偶问题无可行解；若对偶问题无最优解（可以去无穷小），则原问题无可行解。
  • 强对偶定理 (Strong Duality)：若原问题（或对偶问题）有有限最优解，那么对偶问题（或原问题）也有有限最优解，且二者最优解相等。通过单纯形法的计算过程来辅助证明。
  • 互补松弛定理 (Complementary Slackness)：若 $x^\ast$ 与 $y^\ast$ 分别是原问题和对偶问题的可行解，以下两点等价：
    1. $x^\ast$ 和 $y^\ast$ 分别是原问题和对偶问题的最优解；
    2. $(y^{\ast {\rm T}}A - c^{\rm T})x^\ast = 0$ 且 $y^{\ast {\rm T}}(Ax^\ast-b) = 0$。
• 对偶单纯形法步骤（以 $\min$ 模型为例）
  1. 取一组检验数全都 $\ge 0$ 的基。
  2. 找一个 $b_i < 0$ （一般找绝对值最大的）行 $i$，将非基变量 $i$ 出基。
  3. 我们想让某个非基变量从 $0$ 变成大于 $0$ 来增加 $b_i$。在这一行中，找一个 $A_{i,j}< 0$ 的 $j$ 使得 $|\frac{c_j}{A_{i,j}}|$ 最小（这样 $j$ 消完目标函数后检验数依然全都 $\ge 0$），让 $j$ 入基。
  4. 重复步骤 $2 \sim 3$ 直到约束右侧的值均 $\ge 0$ 。
• tsr 讲解对偶单纯形