趣题摘记-奇思妙想

这一系列文章记录了我遇到过的一些趣题。

文章内容	简介
奇思妙想	数学和计算机领域，通过小小思考后能豁然开朗的趣题。
概率和期望	数学和计算机领域，与概率和期望相关的趣题。
算法题精选-1	OI/ICPC 向的算法题，去其琐碎、留其精髓，望博君一笑。
算法题精选-2	OI/ICPC 向的算法题，相比上一期题意更简洁，出处往往不可考

正方形里塞k个尽量大的相同形状

题意：给出正整数 $k$ ，要在一个正方形里塞 $k$ 个相同的正方形/圆，问最多能塞多大的尺寸。

题解：这类问题被称为 Packing problems。很多 $k$ 都还是开放问题，特别当 $k$ 大的时候。Erich Friedman 整理了一个 Packing 合集，包括正方形里塞圆和正方形里塞正方形。

非ww串的文法表达

题意：假设字符集是 $\{0,1\}$ ，用上下文无关语法表达出所有这样的字符串 $S$ ： $S=xy,|x|=|y|,x \ne y$ 。

性质：假设字符串长度为 $2n$ ，则至少存在一个 $i$ ，满足 $S_i \ne S_{n+i}$ 。分别以 $i$ 和 $n+i$ 为中心， $i-1$ 和 $n-i$ 为半径，可以把 $S$ 分成两个中心不同、其余随意的串。ww 串必然不存在这样的划分，而非 ww 串必然存在。

题解： $c=a|b, A=cAc|a, B=cBc|b, S=AB|BA$

翻纸牌

题意：桌面上有两堆扑克牌， $A$ 堆正面朝上的牌比 $B$ 堆多 $50$ 张。你被蒙住了眼睛，只能靠手去触摸和移动牌，无法摸出一张牌是否是正面朝上。如何操作能使 $A$ 堆正面朝上的牌数和 $B$ 堆相同。来源于腾讯面试题。

题解：给人的第一感觉是：既然不能摸出正反面，为什么可以使正面朝上的牌数一致？

考虑如下操作：从 $A$ 堆里摸一张牌，将其翻面后放入 $B$ 堆。

如果它原来是正面朝上的，则 $A$ 堆损失一张正面朝上的牌。
如果它原来是正面朝下的，则 $B$ 堆增加一张正面朝上的牌。

所以每操作这个步骤一次，正面朝上的牌差就减一。重复 $50$ 次后即达到要求。

GCC有关数组的一些函数

1. rotate(first, mid, last): 将 mid 及之后的内容放到 first 前面。
// 实现1：翻转前一段，翻转后一段，再翻转整各数组。
// 实现2：
template <class ForwardIterator>
  void rotate (ForwardIterator first, ForwardIterator middle,
               ForwardIterator last){
  ForwardIterator next = middle;
  while (first!=next){
    swap (*first++,*next++);
    if (next==last) next=middle;
    else if (first==middle) middle=next;
  }
}

2. inplace_merge(first, mid, last)：将 [first, mid) 和 [mid, last) 归并。
// 一种可能的实现
while (fir < mid && mid < last){
  while (fir < mid && a[fir] < a[mid]) ++fir;
  int Move = 0;
  while (mid < last && a[mid] < a[fir]){
    ++mid;
    ++Move;
  }
  rotate(a + fir, a + mid - move, a + mid);
  fir += Move;
}
                                                     
3. inplace_sort(first, mid, last)

只许修改一位的加密解密问题

来源：据传是 Google 面试题，由何柱提供。

题意：Alice 面前有一个长度为 $n$ 的棋盘，初始时每个位置有一个随机的 0/1 值；Alice 还看到一把钥匙随机藏于 $0 \sim n-1$ 的某一个格子。Alice 必须修改一位格子里的 01 值，然后 Bob 只能看到修改后的棋盘状态。Alice 和 Bob 可以事先约定好某种策略，Bob 需要猜出钥匙的所在位置。

解法：可以证明，若 $n$ 不是 $2$ 的幂次就无解。

Alice 观察所有初始值为 $1$ 的格子，将它们的编号异或起来，再异或上 key 的编号。
Bob 观察所有修改后值为 $1$ 的格子，把它们的编号异或起来就是 key 的位置编号。

猜名字

来源：据传是 Google 面试题，由何柱提供。

题意： $n$ 个人的名字互不相同，且知道他们名字的并集 $R$ 。每次可以给出一个人的子集 $S$ ，返回这些人对应的名字集合 $R_S$ 。问最优决策下，询问几次能知道所有人各自对应的名字。

简洁解：不妨设 $n=k^2$ ，把人排成 $k \times k$ 的方阵，分别问每行和每列的答案， $2k$ 次。

最优解：把人名按 $1,\dots,n$ 编号，对于 $k=0 \sim \log_2(n)$ ，询问二进制第 $k$ 位为 $1$ 的那些人的集合。还原答案时只要把该编号对应所有为 $1$ 的答案集合求个交即可。下标为 $0$ 用不了，总次数为 $\lfloor \log_2(n) \rfloor + 1$ 。

严格线性求第k小

题意：给出一个无序数组，试求第 $k$ 小的数是多少，要求严格线性。

近似线性做法：基于快排的分治策略，每次随机一个 $\mathrm{pivot}$ ，按 $\mathbb{pivot}$ 将数组划成两半并递归进其中一半。

$T(N)=\frac{1}{N} \sum \limits_{i=1}^{N}T(i)+O(N)=O(N)$

严格线性做法：定义 $F(A,k)$ 能在 $O(|A|)$ 时间里求出 $A$ 中第 $k$ 小。重复下列三个流程：

将所有数 $5$ 个一组，每组求一个中位数，并将这 $\lceil \frac{N}{5} \rceil$ 个数排成数列 $B$ 。
调用 $F(B,\frac{|B|+1}{2})$ ，求得 $B$ 的中位数 $b$ 。
以 $b$ 为 $\mathrm{pivot}$ 将数组分成两半，并递归进入其中一个 $F(A',k')$ 。

复杂度分析：在复杂度不变的情况下适当定一个 $\mathbb{pivot}$ ，使得每次划分区间时不出现极端情况。我们知道，必然有 $\frac{3N}{10}$ 的数小于 $b$ ，也有 $\frac{3N}{10}$ 的数大于 $b$ ，所以区间最多变成原来的 $O(\frac{7}{10}N)$ 。

$T(N)=T(\frac{N}{5})+T(\frac{7}{10}N)+O(N)=O(N)$

闭区间连续函数的极值

题意：证明对于定义在闭区间 $[a,b]$ 上的连续函数 $f(x)$ ，必然在定义域内存在最小值（和最大值）。

分析：需要证明两件事：

$f(x)$ 在 $[a,b]$ 上有下界。
$f(x)$ 在 $[a,b]$ 上有最小值（这个和 2 不同，因为可能存在取不到下确界的情况）。

证明第一点的方法一：对于任何 $x \in [a,b]$ ，存在 $\epsilon_x$ 使得 $f$ 在 $(x-\epsilon_x,x+\epsilon_x)$ 有界。根据 有限覆盖定理，我们可以取有限个区间覆盖整个 $[a,b]$ 。那么此时每个区域的下界的最大值就是总体的下界。

证明第一点的方法二：反证，假设无界。如果每次将当前区间分成两段，则至少有一段无界，所以我们能得到一个无界的闭区间套 $\{[a_n,b_n]\}$ 。根据 区间套定理，存在唯一实数 $\xi$ 使得 $\xi=\lim \limits_{n \to \infty}a_n=\lim \limits_{n \to \infty} b_n$ 且 $\xi \in [a,b]$ 。但是我们又知道 $f(\xi \pm \epsilon)$ 是有界的，所以对于充分大的 $n$ ， $[a_n,b_n]$ 是有界的。这和题设矛盾。

证明第二点：要用到 最大值最小值定理。假设 $f(x)$ 的下确界是 $M$ ，我们想要证明 $M \in \{f(x) | x \in[a,b]\}$ 是否成立。反证，若取不到下确界则 $f(x)>M$ 。设函数 $g(x,x\in[a,b])=\frac{1}{f(x)-M}$ ，因为 $f(x)$ 连续所以 $g(x)$ 也连续。第一点已证 $g(x)$ 有界，即存在 $G$ 使得 $g(x) \le G$ ，则 $f(x) \ge M+\frac{1}{G}$ ，这和 $M$ 是下确界矛盾。

构造 (0,1) 到 [0,1] 的双射函数

题意：构造从 $(0,1)$ 到 $[0,1]$ 的双射函数？

题解：存在（来源于知乎）。构造集合 $\{\frac{1}{n}|n \ge 2,n \in \mathbb{N}^+\}$ ，定义 $f:(0,1) \rightarrow [0,1]$ 满足：

$f(x)=\left\{ \begin{aligned} x, & x \notin S \\ 0, & x \in S, x=\frac{1}{2} \\ \frac{1}{n-1}, & x \in S, x=\frac{1}{n}(n \ge 3) \\ \end{aligned} \right.$

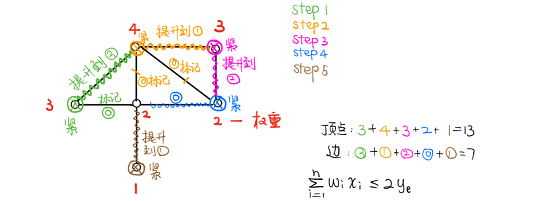
边权最小使指定顶点连通

题意：给定连通无向图 $(V,E)$ 的部分顶点集合 $S$ ，选出边权和最小的边集使得 $S$ 连通。

确定性做法：经典的斯坦纳树问题，复杂度是 $O(n3^n)$ 。设 $f_{S,i}$ 表示使“以 $i$ 为根，点集为 $S$ ”的树连通的最小边权和。对于一种状态 $(S,i)$ ，有两种转移方式：

将 $S$ 拆成两个子集 $S_1$ 和 $S_2$ 转移（相当于这棵树有至少两个子树）。
枚举点 $j$ ，用 $f_{S',j}+E_{j,i}$ 转移（相当于这棵树只有一个子树，枚举子树顶点）。

近似做法：构造一个新图 $(S,F)$ ，对于原图中 $S$ 中的每一对顶点 $(i,j)$ ，连一条边权为 $F_{i,j}$ 的边，其中 $F_{i,j}$ 是原图中 $i$ 到 $j$ 的最短路。在新图上跑一遍 $MST$ 得到一个边集 $E_{result}$ 。显然这组边一定是原图的一个解。

近似度证明：可以证明，上述近似做法的近似度正好是 $2$ 。

考虑一个包含 $S$ 的路径 $P= \{ p_1,p_2,...,p_k \}$ 。任意找出路径上的 $S$ 子序列 $Q= \{ q_1,q_2,...,q_{|S|} \}$ 。 $P$ 中 $q_i \rightarrow q_{i+1}$ 的路径边权和，必然不小于新图中的 $F_{q_i,q_{i+1}}$ 。假设原图最优解的边集是 $E_{answer}$ 。将 $E_{answer}$ 中的每条边都复制一遍，可以得到一张欧拉图，且能导出一个 $P$ 路径。综上， $\sum E_{q_i,q_{i+1}} \geq \sum E_{result}$ ，即 $2\sum E_{answer} \geq \sum E_{result}$ 。
考虑一个边权都相等的菊花图。当 $n \rightarrow +\infty$ 时， $E_{result} \rightarrow 2\sum E_{answer}$ .

最小生成树局部最优等于全局最优

题意：在 MST 问题中，定义一个解的邻域为：删掉一条边并加上一条边后能到达的所有解。求证：MST 问题的一个局部最优解必然是全局最优解。

简化题目：假设所有边权值都不相同。

设局部最优解是 $T$ ，全局最优解是 $T^*$ 。将局部最优解连成一棵树。
反证，假设 $T$ 不是全局最优解。则至少存在一条在 $T^*$ 中的非树边 $E=(u,v)$ 。
在 $T$ 里找到 $u \rightarrow v$ 的路径，依次经过了 $e_1,e_2,...e_k$ 这些边。由条件可知， $\max \limits_{i=1..k} c(e_i) < c(E)$ （否则就不是局部最优解了）。
显然， $u \rightarrow v$ 的路径中，必然存在一条边 $e_i=(p,q)$ ，使得 $p$ 和 $q$ 属于不同的集合。我们在全局最优解里删掉边 $E=(u,v)$ ，加入边 $e_i$ 。全局最优解答案更变得更优，产生矛盾。

所以（任意一个）局部最优解必然是全局最优解。

回到原题：在第 $3$ 步里，条件变成了 $\max \limits_{i=1..k} c(e_i) \leq c(E)$ ；在之前的第 $4$ 步里，有可能会出现 $c(E)=c(e_i)$ ，此时替换边后权值不变，无法导出矛盾。注意到， $T$ 中存在 $e_i$ 不存在 $E$ ， $T^*$ 中存在 $E$ 不存在 $e_i$ 。我们还是做一下边的替换，得到变换后的“等价局部最优解” $T'$ 。经过了这样一次变换后， $T'$ 和 $T^{\ast}$ 之间重复的边增加了一条。重复上述的流程，直到导出反证法的矛盾或是推出 $T'=T^*$ 。

修正：上述的证明过程是有漏洞的。在变换了 $T$ 后，我们并没有证明 $T'$ 在它的邻域也是最优的，就不能应用局部最优解的性质。可以反过来进行修正：

同上述步骤，找到一条非树边 $E$ 。如果 $c(E)=c(e_i)$ ，固定 $T$ 不动，把 $T^\ast$ 里的边 $E$ 替换成 $e_i$ 。
$T$ 和 $T'$ 之间重复的边增加了一条。重复上述的流程，直到导出反证法的矛盾或是推出 $T=T'$ 。

一步到位证明：在取 $T^\ast$ 的时候，我们不妨在所有全局最优解里，取一个 和 $T$ 重复的边最多的解。如果 $T^\ast \ne T$ ，存在一个 $T'$ 使得 $T'$ 里 $T$ 重复的边更近，但是这和 $T^{\ast}$ 矛盾。所以 $T^{\ast}=T$ 。

图的最大割问题

来源：lzw 的博客

题意：给定边权非负的无向图 $G=(V,E)$ ，要将其分成两个点集 $(S, V \backslash S)$ ，最大化 $\sum_{e \in cut(S, V \backslash S)}{w_e}$

基于随机的解：给出一个近似度为 $2$ 的做法。设最优解为 $W$ 。对于每个点, 有 $p$ 的概率选入集合 $S$ ：

$W' = \sum \limits_{e}{w_e \cdot P[e \in (S, V \backslash S)]} = \sum \limits_{e} 2p(1-p)w_e \geq 2p(1-p) W$

取 $p=\frac{1}{2}$ 时有 $W' \geq \frac{1}{2}W$ .

贪心解：初始化集合 $A=B=\emptyset$ 。依次考虑每个点，如果把它加入 $A$ 集合收益更大就加入，否则加入 $B$ 集合。收益指 $\sum \limits_{e \in (A,B)}{w_e}$ 的增量。容易证明在这个过程中始终满足下面的性质:

$\sum \limits_{e \in (A,B)}{w_e} \geq \sum \limits_{e \in (A,A)}{w_e} + \sum \limits_{e \in (B,B)}{w_e}$

从而得出 $W'=\sum \limits_{e \in (A,B)}{w_e} \geq \frac{1}{2}\sum \limits_{e}{w_e} \geq \frac{1}{2}W$ 。

一道初中几何题

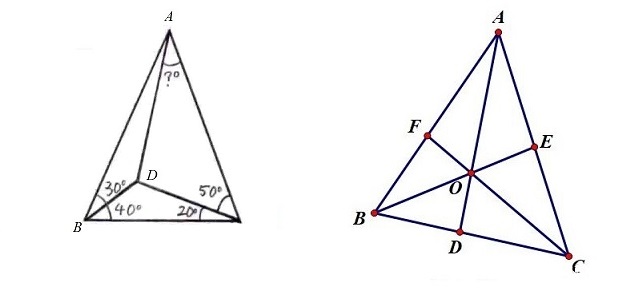
题意：求左图图问号的度数。

背景：塞瓦定理：若 $AD,CF,BE$ 交于 $O$ ，则 $\frac{BD}{DC} \times \frac{CE}{EA} \times \frac{AF}{FB}=1$ （面积法证明）

塞瓦定理的角元形式： $AD,CF,BE$ 交于 $O$ 的充要条件是 $\frac{\sin BAD}{\sin DAC} \times \frac{\sin CBE}{\sin EBA} \times \frac{\sin ACF}{\sin FCB}=1$

题解：把塞瓦定理的角元形式带入得： $\frac{\sin (40-\theta)}{\sin\theta} \times \frac{\sin 40}{\sin 30} \times \frac{\sin 50}{\sin 20}=1$ ，解得 $\theta=30$

公平分蛋糕问题

题意：若干个人要分蛋糕吃。每个人对蛋糕各部分价值的评估是不一样的。有以下两种要求：

公平：每个人都认为，自己得到的部分不低于（自己视角下）总蛋糕价值的 $\frac{1}{n}$ 。
无怨：每个人不觉得别人拿的比自己多。（无怨比公平更难，因为无怨一定公平）

题目和题解均来源于知乎，目前公平分配已解决，多人的无怨分配依旧是开放问题。

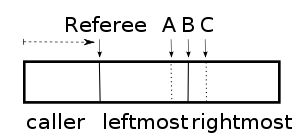
三人无怨的连续解：需要一个裁判，从左向右走刀，三人拿着刀站在裁判右边，保持在（按各自标准）平分右边蛋糕的位置。任何时刻一旦三人中有一个喊「切」，此人获得裁判左边的蛋糕。然后三人中位于中间位置的那位（B）把刀切下。没蛋糕的两位中，离裁判近的那位获得中间那块，远的那位获得右边那块。

三人无怨的离散解法：

A 按照自己的标准把蛋糕切三块。
如果 B 认为最大的两块一样大，那么按 C，B，A 的顺序选蛋糕，结束。
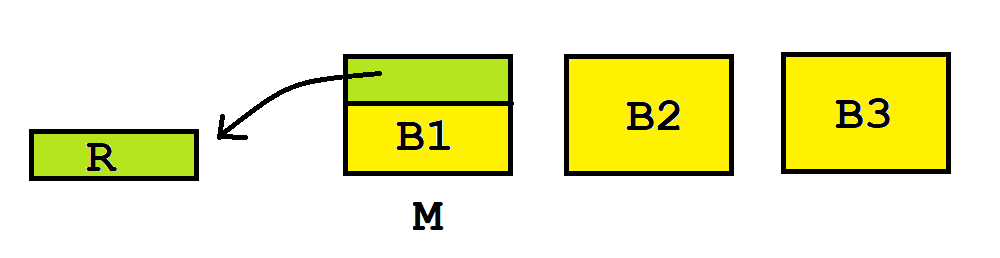
如果 B 认为其中一块 M 最大，他就从 M 削去一小块 R，使之与第二大的那块一样，把 R 放在一边。
称 M 剩下的部分为 M'。
按 C，B，A 的顺序选这三块蛋糕，但有个要求是，如果 C 没有选走 M'，B 须被迫选走它。
B 和 C 中没拿 M' 的那位，把 R 分成三份，让拿了 M' 的那位先挑一份，然后 A 选一份，最后一份留给自己。

上述做法的分析：

先来证明 C 的无怨。第一轮选择的时候他有最优先权：如果他认为 B1（即算法里的 M'）最优，那么它在第一轮能先选走自己认为最大的，而且可以在第二轮均分蛋糕，使得第二轮自己也能拿 R 中至少 1/3，肯定是无怨的；如果他认为 B2 或者 B3 最优，它将在两轮选蛋糕里都最先选走自己认为的最大的，显然无怨。
再来证明 B 的无怨。经过削蛋糕操作后，他眼中 B1=B2>B3——所以如果 C 选走了 B1 或 B2 中的任意一个，B 将选走它们中的另一个（C 选走 B3 的话，B 被迫选走 B1 也不亏）。而且在第二轮里，B 拥有切或者先选的权力，分析同上，也是无怨的。
再来证明 A 的无怨。A 一开始在切的时候，是把蛋糕按照自己的标准均分的，所以在他眼中，B2=B3>B1。由规则保证，第一轮分蛋糕时 B1 一定会被选走，所以在第一轮中， A 尽管获得剩下的蛋糕，也是无怨的。此时在 A 眼中，拿了 B1 的人最后的总价值超不过他，他只需在第二轮中考虑剩下的那个人。没拿 B1 的人将在第三轮最后选，所以 A 挑剩下两块中自认为价值大的，他获得的总价值也不会低于没拿 B1 的人。