论文调研：图的最小圈基

最小环基（Minimal Cycle Basis，中文翻译是我随便取的）是图论的一个具体的研究问题。借着华为 Hackathon 2023 的机会，我决定对学界的 Minimal Cycle Basis 问题做一次系统性地调研。

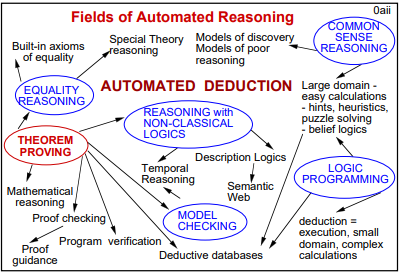
概念和记号表示

考虑不存在重边、自环的无向/有向图 $G=(V,E)$，点没有权重，边可以有权重。

记号	含义
$n,m$	图 $G$ 中的点数和边数，即 $n=
$x,y$	图 $G$ 中的某两个顶点，即 $x,y \in V$
$e$	图 $G$ 中的某条边，即 $e \in E$
$P(x,y)$	从 $x$ 到 $y$ 的某条最短路径的边集
$B$	$G$ 的某一个环基
$C$	$G$ 的某一个环
$T$	$G$ 的某一个生成树
$T_x$	$G$ 中以 $x$ 为根的最短路径树

环：环是一个边的子集，满足导出子图连通且每个点的度数都是偶数。简单环 额外要求每个点的度数都是 $2$。

环的和：对于两个环 $C_1,C_2$，定义它们的 和 为这两个集合的对称差，即 $C_{sum}=(C_1 \cup C_2)-(C_1 \cap C_2)$，简记为 $C_{sum}=C_1+C_2$。容易发现，两个环的和一定是空集、一个合法的环或两个不相交的环。

环的向量表示：我们可以用一个长度为 $|V|$ 的 01 向量 $v$ 表示一个简单环，$v_i=1$ 当且仅当环中包含点 $i$。那么两个环的和的向量表示是 $v_{sum}=v_1 \oplus v_2$。

环空间：对于环集 $D_0=\{C_1,C_2,\dots,C_l\}$，设环集序列 $D_i=\{C_i + C_j | C_i,C_j \in D_{i-1}\}$，称 $D_{+\infty}$ 为环集 $C$ 导出的环空间。显然有 $D_{+\infty}=\{k_1C_1+k_2C_2+\dots+k_lC_l\}$，其中 $k_i=\{0,1\}$。

环基：环空间覆盖了图上所有环的环集成为环基。环基里每一个环的向量都是线性无关的，而且它们能线性表出整个环空间。设 $B$ 是一组环基，则有 $|B|=m-n+1$。边权和最小的环基即为 最小环基。

Horton 1984：第一个多项式做法

对于边可以带权的 无向图，提出了 MCB 的第一个多项式做法，复杂度为 $O(m^3n)$。

定理 0：若 $C \in B$ 且 $C=C_1+C_2$，那么环集 $(B-C) \cup C_1$ 和环集 $(B-C) \cup C_2$ 一定有一个是环基。

定理 1：环基中一定存在一个环 $C$ 满足 $C$ 是最小环。

定理 2：若 $C \in B$ 且 $x,y \in C$，那么 $P(x,y) \subseteq C$。

定理 3：若 $C \in B$，对于任何 $x \in C$，存在 $e=(y,z)$ 使得 $C=P(x,y) \cup P(x,z) \cup \{e\}$。

定理 4：若 $e=(x,y)$，包含 $e$ 的最小环 $C_e$ 满足 $C_e$ 在某一个合法环基里。

基本算法：按下列步骤可以求得一个 $G$ 的环基：

1. 对于所有点对 $(x,y)$，计算 $P(x,y)$。
2. 枚举所有点边对 $v,(x,y)$，创建环 $C(v,x,y)=P(v,x) \cup P(v,y) \cup \{(x,y)\}$。
3. 按边权和从大到小枚举每一个环，能选就选。用高斯消元来判定。

复杂度分析：第 2 步会构造出 $O(nm)$ 个环。每个环用向量表示，构成了 $O(nm) \times m$ 的矩阵。第 3 步里从前往后枚举每一行，如果不是全零就选上，然后向后做一遍消元。不妨设环基的元素个数是 $d=m-n+1$，总共会消元 $O(nm) \times d$ 次，单次消元涉及 $m$ 列，所以总复杂度为 $O(dm^2n)=O(m^3n)$。

加速：第 2 步生成环 $C=\{x_1,x_2,\dots,x_k\}$ 后，可以花 $O(k)$ 的时间利用定理 3 来检查这个环是否值得被尝试。具体来说，设 $r_i(1 \le i \le k)$ 为 $x_i$ 向右最远衍生到的环上的点使得 $P(x_i,r_i)=\{x_i,x_{i+1},\dots,r_i\}$，同理 $l_i$ 是向左最远衍生的环点。当前环能在最小环基中的必要条件：对于任何 $1 \le i \le k$，$(l_i,r_i)$ 是相邻的。利用这个性质可以对环进行提早剪枝，但作者并不会证明是否能降低复杂度。注意这个条件并不充分，存在相应的反例。

Pina 1995：基于代数图论

对于边可以带权的 无向图，提出了一个 $O(m^3+m^2n \log n)$ 的基于代数图论的做法。

代数表示：任取 $G$ 的一棵生成树 $T$，$E_{G \backslash T}$ 是 $G$ 的非树边集合，不妨设 $N=|E_{G \backslash T}|$。对于图中任意一个环 $C$，可以用 $\{0,1\}^N$ 空间下的向量 $v$ 来表示：$1$ 表示包含这条非树边而 $0$ 表示不包含。

内积：定义 $\langle u,v\rangle$ 为两个环向量在 $GF(2)$ 下的内积。$\langle u,v\rangle=1$ 当且仅当环 $u$ 和环 $v$ 有奇数条公共边。

支持向量：环集 $\{C_1,C_2,\dots,C_{i-1}\}$ 的支持向量 $S_i$ 满足：$S_i$ 非平凡（$S_i \ne \mathbb{0}$）且 $S_i$ 与所有 $C_j$ 正交。

总体算法：假设当前已找到环基的前 $i-1$ 个环 $\{C_1,C_2,\dots,C_{i-1}\}$，求出它们的任一支持向量 $S_i$：

$$\langle C_k,S_i \rangle = 0, \quad k=1,2,\dots,i-1$$

在图中找到一个边权和最小的环 $C_i$ 使得 $\langle C_i,S_i \rangle=1$，将其加入集合。重复操作直到加入 $m-n+1$ 个环。

找正交环：把图中所有点 $v \in V$ 拆成 $(v_0,v_1)$ 左右两个点，构造新图。枚举 $e=(u,v) \in G \backslash T$，如果 $e \in S_i$ 就连接 $(u_0, v_1)$ 和 $(u_1,v_0)$ 两条边，否则连接 $(u_0,v_0)$ 和 $(u_1,v_1)$ 两条边。断言：新图中从任意 $v_0$ 出发抵达 $v_1$ 的路径，正好对应原图中包含 $v$ 且与 $S_i$ 正交的环。需要对枚举所有 $(v_0,v_1)$ 找出最短路径，这是多源最短路。

维护支持向量：初始时设 $S_i=\{e_i\}(1 \le i \le N)$，这样所有支持向量彼此之间正交。增加 $C_i$ 后更新 $S_j$：

$$S'_j=\left\{ \begin{aligned} S_j \quad & \langle C_i,S_j \rangle =0 \\ S_j+S_i \quad & \langle C_i,S_j \rangle =1 \end{aligned} \right. \quad i+1 \le j \le N$$

更新完后能保证 $S'_{i+1},S'_{i+2},\dots,S_N$ 是完全正交于 $C_1,C_2,\dots,C_i$ 的子空间。

复杂度分析：每一步求 $C_i$ 的复杂度是多源最短路，需要跑 $n$ 遍堆优化的 Dijkstra，复杂度 $O(nm \log n)$；每一步更新 $S_{i+1},S_{i+2},\dots,S_N$ 的复杂度是 $O(m^2)$。重复 $m-n+1$ 次，总复杂度为 $O(m^3+mn^2 \log n)$。

Kavitha 2004：分治加速支持向量

在 Pina 1995 的基础上，优化了求支持向量的部分，提出了复杂度为 $O(m^\omega+m^2n+mn^2 \log n)$ 的分治做法。当多源最短路退化时：整数边权的复杂度降低至 $O(m^2n)$，而边不带权的复杂度进一步降低至 $O(m^\omega)$。

分治：设 $F(\{C_1,C_2,\dots,C_i\}, \{S_{i+1},S_{i+2},\dots,S_{i+k}\}, k)$ 表示在前 $i$ 个环已经形成，$\{S_{i+1},S_{i+2},\dots,S_{i+k}\}$ 这些支持向量已正交于前 $i$ 个环，在此基础上求出 $\{C_{i+1},C_{i+2},\dots,C_{i+k}\}$ 这些环。

• 最外层调用 $F(\emptyset,\{~\{e_1\},\{e_2\},\dots,\{e_N\}~\},N)$ 即为答案。
• 若 $k=1$，此时 $S_{i+1}$ 一定已维护准确。重复找正交环的过程求出满足 $\langle C_{i+1},S_{i+1} \rangle$ 的 $C_{i+1}$ 即可。
• 若 $k>1$，那么将 $\{S_{i+1},S_{i+2},\dots,S_{i+k}\}$ 拆成两半 $\{S_{i+1},S_{i+2},\dots,S_{i+mid}\}$ 和 $\{S_{i+mid+1},\dots,S_{i+k}\}$。
  1. 调 $F(\{C_1,C_2,\dots,C_i\}, \{S_{i+1},S_{i+2},\dots,S_{i+mid}\}, mid)$ 求出前 $mid$ 个环和支持向量。不妨设更新后的支持向量为 $\{T_{i+1},T_{i+2},\dots,T_{i+mid}\}$。显然 $\{T_{i+1},T_{i+2},\dots,T_{i+mid}\}$ 都正交于 $\{C_1,C_2,\dots,C_i\}$。
  2. 利用 $\{C_1,C_2,\dots,C_i\}$ 和 $\{T_{i+1},T_{i+2},\dots,T_{i+mid}\}$ 去更新后半段的 $\{S_{i+mid+1},\dots,S_{i+k}\}$。
  3. 调 $F(\{C_1,C_2,\dots,C_i\}, \{T_{i+mid+1},T_{i+mid+2},\dots,T_{i+k}\}, k-mid)$ 求出后 $k-mid$ 个环和支持向量。

考虑 $k>1$ 的第 2 步。我们希望更新 $\{S_{i+mid+1},\dots,S_{i+k}\}$ 使其能正交于 $\{C_{i+1},C_{i+2},\dots,C_{i+mid}\}$。构造：

$$T_j=S_j+a_{j,1}T_{i+1}+a_{j,2}T_{i+2}+\dots+a_{j,mid}T_{i+mid} \quad mid<j \le k$$

注意到 $S_j$ 和 $\{T_{i+1},T_{i+2},\dots,T_{i+mid}\}$ 本都正交于 $\{C_1,C_2,\dots,C_{i}\}$，所以 $T_j$ 一定与之正交。我们有 $mid$ 个自由系数 $\{ a_{j,1},\dots,a_{j,mid} \}$ 可以确定，想要使 $T_j$ 正交于 $mid$ 个新环 $\{C_{i+1},C_{i+2},\dots,C_{i+mid} \}$，这是能办到的。

$$AX+Y=0,X=\left\{\begin{aligned} \langle T_{i+1},C_{i+1} \rangle ~\dots & ~\langle T_{i+1},C_{i+mid} \rangle \\ \langle T_{i+2},C_{i+2} \rangle ~\dots & ~\langle T_{i+2},C_{i+mid} \rangle \\ \dots & \\ \langle T_{i+mid},C_{i+2} \rangle ~\dots & ~\langle T_{i+mid},C_{i+mid} \rangle \\ \end{aligned} \right\}, Y=\left\{\begin{aligned} \langle T_{i+mid+1},C_{i+1} \rangle ~\dots & ~\langle T_{i+mid+1},C_{i+mid} \rangle \\ \dots & \\ \langle T_{i+k},C_{i+2} \rangle ~\dots & ~\langle T_{i+k},C_{i+mid} \rangle \\ \end{aligned} \right\}$$

注意 $X$ 是上三角矩阵（左下块全 $0$），即 $X$ 一定可逆。系数矩阵 $A=YX^{-1}$。

分治复杂度分析：根据主定理，下列分治式子的综合复杂度为 $O(m^2n+mn^2 \log n)$。

$$X=\left\{\begin{aligned} mn+n^2 \log n & \quad k=1 \\ 2T(k/2)+O(k^{\omega-1}m) & \quad k>1 \end{aligned} \right.$$

$\alpha-$近似算法：在每一轮找 $\langle S_i,C_i\rangle$ 的最小环时 ，如果找到的环 $D_i$ 满足 $w(D_i) \le \alpha \cdot w(C_i)$，那么所得的环基 $\{D_1,D_2,\dots,D_N\}$ 的一定也满足 $\sum w(D_i) \le \alpha \cdot MCB$。证明比较复杂，这里略过。以 $\alpha=2$ 为例，利用 Cohen2001 的 $2-$近似最短路，$2-$ 近似 MCB 的时间复杂度为 $O(m^{1.5}n^{1.5}+m^\omega)$。

验证环基：直接套用分治做法计算 $S_i$ 可以验证 $\{C_1,C_2,\dots,C_N\}$ 是否是环基，复杂度为 $O(m^\omega)$。

Mehlhorn 2007：加速找环

在 Pina 1995 和 Kavitha 2004 的基础上，优化了根据 $S_i$ 找 $C_i$ 的步骤，提出了复杂度为 $O(m^2n / \log n+n^2m)$ 的无向图带权 MCB 做法，注意分治求 $S_i$ 的部分还在，但是 $O(m^\omega)$ 可以视为被 $O(m^2n/\log n)$ 覆盖。

优化备选环集：Horton 1984 提出了一种大小为 $O(nm)$ 的备选环集，即枚举任意点和任意边，用它们之间的最短路径构造环，记为 $C[w,e]$。本文分别从点和边的角度优化了备选环集的大小（并没有实质性地降低复杂度）：

• 从点的角度来说：我们只需考虑所有被环覆盖的点的点集，即 $Z=\{C_1 \cup C_2 \cup \dots\}$。最坏情况下 $Z=V$。准确地求 $Z$ 是一件很难的事情，不过 Bafna1999 给出了一种无向图 $2-$近似的 $Z'$ 集合求法。
• 从边的角度来说：当枚举的点是 $z \in Z$ 时，设 $T_{z}$ 是以 $z$ 为根的最短路径树，我们只需枚举所有满足下列要求的非树边 $(u,v)$ 来构造环集：$u$ 和 $v$ 在 $T_z$ 上的最近公共祖先等于 $z$。证明比较复杂，这里略过了。

优化找环算法：构造上述备选环集后，把这些环按边权从小到大排序，复杂度是 $O(nm \log n)$。在第 $i$ 步时，我们希望在有序的环数组中找到最靠前的 $C_i$ 使得 $\langle S_i,C_i\rangle=1$。

1. 枚举所有点 $z \in Z$，在 $T_z$ 上计算出从根 $z$ 到每个节点的前缀内积，即预处理 $l_z(x)=\langle S_i,Path(z,x) \rangle$，其中 $Path(z,w)$ 表示 $z \sim w$ 树上路径构成的点集。这一步预处理的复杂度是 $O(n|Z|)=O(n^2)$。
2. 按顺序枚举每一个环 $C[z,e=(u,v)]$，利用 $l_z(u) \oplus l_z(v) \oplus [e \in S_i]$ 来 $O(1)$ 计算出这个环和 $S_i$ 的内积。这一步枚举的复杂度是 $O(m|Z|)=O(nm)$。

上述过程总共持续 $m-n+1$ 步，所以总复杂度为 $O(m^2n+m^\omega)$，比 Pina 1995 的做法更快更简单。

进一步优化：利用 bitset 的思想能进一步优化上述过程 。在第 $i$ 步时：

1. 同样花 $O(n|Z|)$ 预处理出 $T_z(x)$，维护 $n$ 个 01 向量 $H_i$ 满足 $H_x=\{T_z(x)|z \in Z\}$。
2. 对于每条边 $e=(u,v)$，把待选点集 $z \in Z$ 按每 $2^b$ 个分块。假设某块的点集是 $B$，枚举所有的 $A \subseteq B$ 并记录 $i_{e,B}(A)=x,x \in A~\wedge~w(C[x,e])=\min(\{w(C[z,e])|z \in A\})$。预处理复杂度 $O(mn2^b)$。
3. 枚举每条边 $e=(u,v)$，计算 $L=H_u \oplus H_v \oplus O$，其中 $O$ 表示全 1 或全 0 向量，取决于 $\langle \{e\},S_i \rangle$ 的值。对于每一个待选点集块 $B$，假设 $L$ 在这块上的答案是 $L_B$，说明所有 $z \in L_B$ 的点 $z$ 能使 $\langle C[z,e], S_i \rangle=1$。此时我们利用之前预处理的 $i_{e,B}(L_B)$ 来快速定位环长最小的环。整体的扫描复杂度 $O(nm/b)$。

综上，总复杂度 $O(nm2^b+m(n^2+nm/b)+m^\omega)$，取 $b=\frac{1}{2} \log n$ 时复杂度为 $O(m^2n / \log n+mn^2)$。

Amaldi 2009：蒙特卡洛

论文标题很霸气，叫做 Breaking the $O(m^2n)$ Barrier for Minimum Cycle Bases。Kavitha 2004 把维护支持向量的复杂度降低为 $O(m^\omega)$，而本文优化了找边权最小的 $\langle C_i,S_i \rangle=1$ 的部分，总复杂度是非确定性的 $O(m^\omega)$。

推广：内积、正交等逻辑可以从 $GF(2)$ 推广成 $GF(p)$（$p$ 是一个素数）。维护支持向量的公式推广为：

$$S_j=S_j-\frac{\langle C_i,S_j \rangle}{\langle C_i,S_i \rangle}S_i$$

无向图最小环基取 $p=2$，有向图取 $p=O(m)$，所以 $GF(p)$ 上的加减乘除运算都视为 $O(1)$。

环集快速判定问题：对于一个环 $C$，我们可以 $O(m)$ 计算出它是否和目标向量 $S_i$ 正交（$\langle C,S_i \rangle=0$）。那么对于一个环的集合 $G$，能否以低于 $O(|G|m)$ 的复杂度，快速判定是否集合里的所有环都和目标向量 $S_i$ 正交。

环集快速判定算法：对环集 $G$ 里的每个环 $C$，取固定系数 $\lambda_C \in GF(p)$，那么我们可以求出环集 $G$ 的“代表向量” $R_G=\sum_{C \in G} \lambda_CC$。当 $\langle C,S_i \rangle \ne 0$ 时，必然存在 $C \in G$ 使得 $C$ 和 $S_i$ 不正交；反之，我们声明环集内的所有环都和 $S_i$ 正交，错误概率是 $P(err)=1/p$。若 $\lambda_C$ 重复取 $k$ 组，出错概率降低到 $P(err)=p^{-k}$。

找最小环算法：将 $O(nm)$ 个备选环按边权大小构建一颗二叉平衡树，深度 $O(\log nm)=O(\log n)$。对于树上的每一个环 $C$，我们都随机 $k$ 组 $\lambda_C$，预处理它的整个子树环集里的代表向量（总共也有 $k$ 组）。每当我们想找边权和最小的 $C_i$ 使得 $\langle C_i,S_i \rangle=1$ 时，从平衡树的根节点出发，每次询问左儿子的环集里是否所有环都和 $S_i$ 正交，如果不是则往左走（这一步不会出错），如果是则往右走（这一步有 $p^{-k}$ 的概率出错），走完树高即能贪心地确认本次的 $C_i$。总共有 $O(m)$ 个需要确认，总决策数 $O(m \log n)$，错误概率 $P(err)=m \log nm \cdot p^{-k}$。每次决策都要重复计算 $k$ 次，每次耗时 $O(m)$，所以找最小环算法的总复杂度是 $O(km^2\log n)$。

笔者注：错误概率应以指数体现，可能作者默认 $p^{-k}$ 很小小，所以 $(1-p^{-k})^{m \log n}$ 用 $m \log n \cdot p^{-k}$ 近似。

总结：利用上述蒙特卡洛随机算法，总时间复杂度为 $O(nm+n^2\log n+m^\omega+km^2\log n)$，简化为 $O(m^\omega)$。错误概率 $P(err)=m \log (nm)p^{-k}$，$m$ 足够大时取 $k=m^{0.1}$，错误概率可以忽略不计。

Rathod 2021 更简洁的非确定性做法

本文同时做了 Minimum Cycle Basis 和 Minimum Homology Basis，前者给出了一个 $\tilde{O}(m^\omega)$ 的做法。

利用 Pina 1995 的分析结论，对 $O(nm)$ 个备选环按边权和从小到大排序，并构成一个 $m \times n$ 的矩阵 $A$，显然该矩阵的秩为 $r=m-n+1$。现在定义 colomn(row) rank profile 为：字典序最小的列（行）下标 $[i_1,i_2,\dots,i_r]$ 使得这些列（行）线性无关。可以用反证法证明：$[A_{i_1},A_{i_2},\dots,A_{i_r}]$ 即为一组最小环基。

高斯消元求 rank profile 是 $O(nmr)$ 的，而已知复杂度最低的确定性做法是 $O(mnr^{\omega-2})$ 的。

Cheung 2013 提出了一个突破性的蒙特卡洛算法（但求出的列不是字典序最小的），复杂度记为：

$$O(nnz(A)+r^\omega)^{1+o(1)}=\tilde{O}(nnz(A)+r^\omega)$$

其中 $o(1)$ 表示一些 $\log n$ 和 $\log m$ 的系数，$nnz(A)$ 表示矩阵的非零元素个数，$\tilde{O}$ 表示忽略一些多项式小因子。

Storjohann 和 Yang 在 2014 年以同样的 $\tilde{O}(nnz(A)+r^\omega)$ 复杂度求出了 rank profile，错误概率 $1/2$。

利用上述研究成果，对备选环排序、构建矩阵、求 rank profile 后，即可在 $\tilde{O}(m^\omega)$ 的时间内求出最小环基。