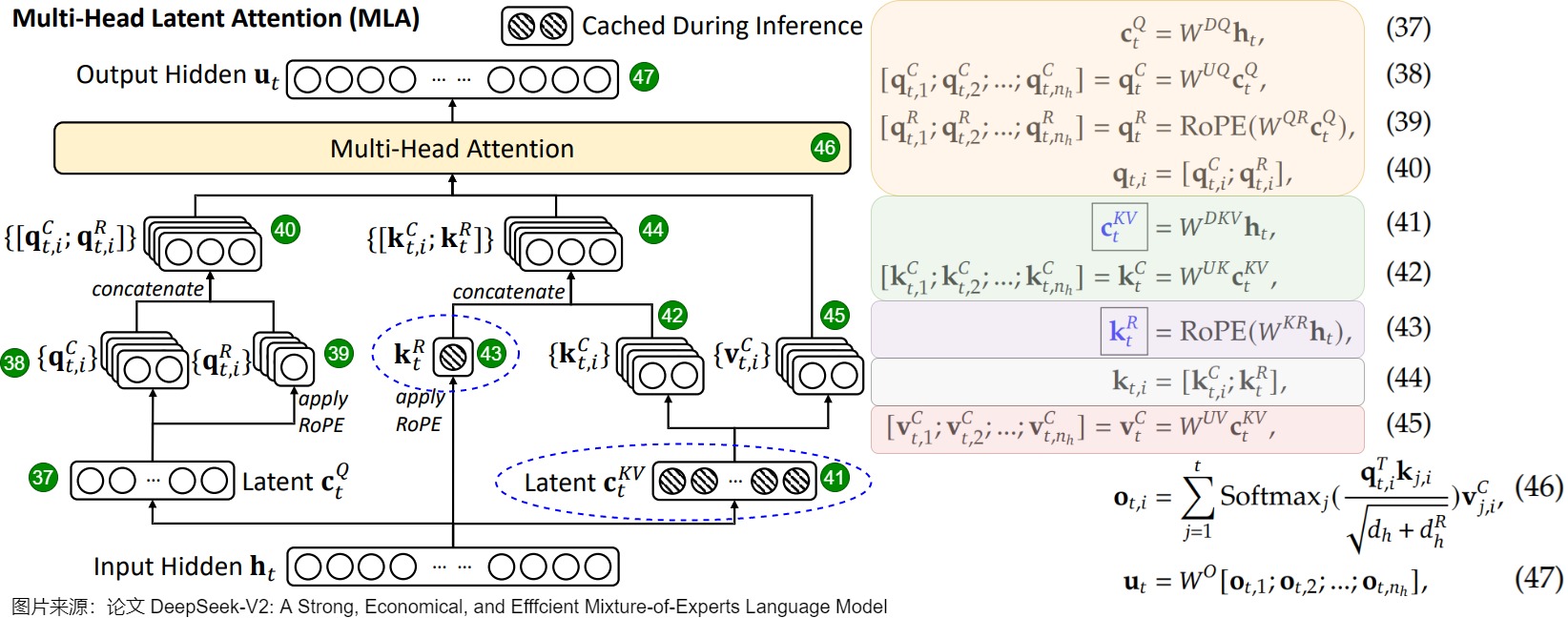
MLA 机制

这一章主要参考苏剑林老师的科学空间博文：缓存与效果的极限拉扯：从MHA、MQA、GQA到MLA。

MHA

Multi-Head Attention 指的就是多头注意力，是开山之作 Attention is all you need 中所提出的一种注意力机制。下面考虑增量模式下的 MHA 计算公式（方便起见，已忽略 qkT\boldsymbol{q}\boldsymbol{k}^T 除以 dk\sqrt{d_k} 的归一化步骤） 。不妨设输入的行向量序列为 (x1,x2,…,xt),xi∈Rd(\boldsymbol{x}_1,\boldsymbol{x}_2,\dots,\boldsymbol{x}_t),x_i \in \mathbb{R}^{d}，现在要计算 Attention 层的结果 ot\boldsymbol{o}_t。用 1≤s≤h1 \le s \le h 表示某个注意力头。

ot(s)=Attention(qt(s),k≤t(s),v≤t(s))≜∑i≤texp⁡(qt(s)ki(s)⊤)vi(s)∑i≤texp⁡(qt(s)ki(s)⊤)qi(s)=xiWq(s)∈Rdk,Wq(s)∈Rd×dkki(s)=xiWk(s)∈Rdk,Wk(s)∈Rd×dkvi(s)=xiWv(s)∈Rdv,Wv(s)∈Rd×dv\begin{equation} \begin{gathered} \boldsymbol{o}_t^{(s)} = Attention\left(\boldsymbol{q}_t^{(s)}, \boldsymbol{k}_{\leq t}^{(s)} ,\boldsymbol{v}_{\leq t}^{(s)}\right)\triangleq\frac{\sum_{i\leq t}\exp\left(\boldsymbol{q}_t^{(s)} \boldsymbol{k}_i^{(s)}{}^{\top}\right)\boldsymbol{v}_i^{(s)}}{\sum_{i\leq t}\exp\left(\boldsymbol{q}_t^{(s)} \boldsymbol{k}_i^{(s)}{}^{\top}\right)} \\[15pt] \boldsymbol{q}_i^{(s)} = \boldsymbol{x}_i\boldsymbol{W}_q^{(s)}\in\mathbb{R}^{d_k},\quad \boldsymbol{W}_q^{(s)}\in\mathbb{R}^{d\times d_k}\\ \boldsymbol{k}_i^{(s)} = \boldsymbol{x}_i\boldsymbol{W}_k^{(s)}\in\mathbb{R}^{d_k},\quad \boldsymbol{W}_k^{(s)}\in\mathbb{R}^{d\times d_k} \\ \boldsymbol{v}_i^{(s)} = \boldsymbol{x}_i\boldsymbol{W}_v^{(s)}\in\mathbb{R}^{d_v},\quad \boldsymbol{W}_v^{(s)}\in\mathbb{R}^{d\times d_v} \end{gathered} \end{equation}

实践上，常见的设置是 dk=dv=d/hd_k = d_v = d / h。对于 LLAMA2-7B 有 d=4096,h=32,dk=dv=128d=4096, h=32, d_k = d_v = 128，LLAMA2-70B则是 d=8192,h=64,dk=dv=128d=8192,h=64, d_k = d_v = 128。

预测后续所有 token 时，k≤t(s),v≤t(s)\boldsymbol{k}_{\leq t}^{(s)} ,\boldsymbol{v}_{\leq t}^{(s)} 的值一直保持不变，这部分结果就可以缓存下来供后续生成调用，以避免不必要的重复计算，这就是所谓的 KV Cache。当模型参数量变大后，每个 Attention 结构要耗费 d×(dk+dv)×hd \times (d_k+d_v) \times h 大小的存储空间，因此就推出了 Multi-Query Attention 和 Grouped-Query Attention 来优化显存。MQA 将 KV Cache 全部重复使用（即 k1(s)=⋯=kt(s),v1(s)=…,=vt(s)\boldsymbol{k}_1^{(s)}=\dots=\boldsymbol{k}_t^{(s)},\boldsymbol{v}_1^{(s)}=\dots,=\boldsymbol{v}_t^{(s)} ），而 GQA 则将其分组重复使用。

MLA 缘起

MLA（Multi-head Latent Attention）应用于 DeepSeek V2 和 V3，利用低秩分解和矩阵吸收来减少 MHA 的 KV Cache 占用，同时让效果不逊于 MQA 和 GQA。其核心思想是引入了 Wc\boldsymbol{W}_c 和 ci\boldsymbol{c}_i：

ci=xiWc∈Rdc,Wc∈Rd×dcqi(s)=xiWq(s)∈Rdk,Wq(s)∈Rd×dkki(s)=ciWk(s)∈Rdk,Wk(s)∈Rdc×dkvi(s)=ciWv(s)∈Rdv,Wv(s)∈Rdc×dv\begin{equation} \begin{gathered} \boldsymbol{c}_i = \boldsymbol{x}_i \boldsymbol{W}_c\in\mathbb{R}^{d_c},\quad \boldsymbol{W}_c\in\mathbb{R}^{d\times d_c} \\[10pt] \boldsymbol{q}_i^{(s)} = \boldsymbol{x}_i\boldsymbol{W}_q^{(s)}\in\mathbb{R}^{d_k},\quad \boldsymbol{W}_q^{(s)}\in\mathbb{R}^{d\times d_k}\\ \boldsymbol{k}_i^{(s)} = \boldsymbol{c}_i\boldsymbol{W}_k^{(s)}\in\mathbb{R}^{d_k},\quad \boldsymbol{W}_k^{(s)}\in\mathbb{R}^{d_c\times d_k} \\ \boldsymbol{v}_i^{(s)} = \boldsymbol{c}_i\boldsymbol{W}_v^{(s)}\in\mathbb{R}^{d_v},\quad \boldsymbol{W}_v^{(s)}\in\mathbb{R}^{d_c\times d_v} \end{gathered} \end{equation}

上述形式在推理时仍然要缓存彼此不同的 ki(s)\boldsymbol{k}_i^{(s)} 和 vi(s)\boldsymbol{v}_i^{(s)}。注意到以下恒等变换：

qt(s)ki(s)⊤=(xtWq(s))(ciWk(s))⊤=xt(Wq(s)Wk(s)⊤)ci⊤\begin{equation}\boldsymbol{q}_t^{(s)} \boldsymbol{k}_i^{(s)}{}^{\top} = \left(\boldsymbol{x}_t\boldsymbol{W}_q^{(s)}\right) \left(\boldsymbol{c}_i\boldsymbol{W}_k^{(s)}\right){}^{\top} = \boldsymbol{x}_t\left(\boldsymbol{W}_q^{(s)}\boldsymbol{W}_k^{(s)}{}^{\top}\right)\boldsymbol{c}_i^{\top} \end{equation} \\

如果用 Wqk(s)=Wq(s)Wk(s)⊤\boldsymbol{W}_{qk}^{(s)}=\boldsymbol{W}_q^{(s)}\boldsymbol{W}_k^{(s)}{}^{\top} 替换 Wq(s)\boldsymbol{W}_q^{(s)} ，MHA 里的 ki(s)\boldsymbol{k}_i^{(s)} 就能视为此处的 ci\boldsymbol{c}_i，这样后者可以在不同注意力头之间共享——我们称这种变换为 吸收变换。MHA 的 vi(s)\boldsymbol{v}_i^{(s)} 同样能做吸收变换视为 ci\boldsymbol{c}_i，因为 ot(s)\boldsymbol{o}_t^{(s)} 最后会拼起来过一遍投影矩阵 [ot(1),ot(2),…,ot(h)]WO,WO∈Rdvh×d[\boldsymbol{o}_t^{(1)},\boldsymbol{o}_t^{(2)},\dots,\boldsymbol{o}_t^{(h)}]\boldsymbol{W}_O,\quad \boldsymbol{W}_O \in\mathbb{R}^{d_vh\times d}，所以 Wv(s)\boldsymbol{W}_v^{(s)} 可以和 WO(s)\boldsymbol{W}_O^{(s)} 合并。

注意：吸收变换虽然在数学上等价，在低精度运算下误差会增大。

兼容 RoPE

DeepSeek 使用了 RoPE 这种“用绝对坐标包含相对关系”的位置编码。RoPE 是 dk×dkd_k \times d_k 的分块对角矩阵 Rm\boldsymbol{\mathcal{R}}_m，满足 RmRn⊤=Rm−n\boldsymbol{\mathcal{R}}_m\boldsymbol{\mathcal{R}}_n^{\top}=\boldsymbol{\mathcal{R}}_{m-n}。加上 RoPE 后无法进行吸收减缓，因为两个 W\boldsymbol{W} 之间会出现和位置相关的 Rt−i\boldsymbol{\mathcal{R}}_{t-i} 项：

qi(s)=xiWq(s)Ri,ki(s)=ciWk(s)Riqt(s)ki(s)⊤=(xtWq(s)Rt)(ciWk(s)Ri)⊤=xt(Wq(s)Rt−iWk(s)⊤)ci⊤\begin{equation} \boldsymbol{q}_i^{(s)} = \boldsymbol{x}_i\boldsymbol{W}_q^{(s)}{\boldsymbol{\mathcal{R}}_i}\quad,\quad\boldsymbol{k}_i^{(s)} = \boldsymbol{c}_i\boldsymbol{W}_k^{(s)}{\boldsymbol{\mathcal{R}}_i} \\ \boldsymbol{q}_t^{(s)} \boldsymbol{k}_i^{(s)}{}^{\top} = \left(\boldsymbol{x}_t\boldsymbol{W}_q^{(s)}{\boldsymbol{\mathcal{R}}_t}\right) \left(\boldsymbol{c}_i\boldsymbol{W}_k^{(s)}{\boldsymbol{\mathcal{R}}_i}\right){}^{\top} = \boldsymbol{x}_t\left(\boldsymbol{W}_q^{(s)}{\boldsymbol{\mathcal{R}}_{t-i}} \boldsymbol{W}_k^{(s)}{}^{\top}\right)\boldsymbol{c}_i^{\top} \end{equation}

MLA 的解决方法是将 qi\boldsymbol{q}_i 和 ki\boldsymbol{k}_i 的维度从 dkd_k 扩展到 dk+drd_k+d_r，其中 drd_r 是专为兼容 RoPE 而设计的，即这部分无法进行吸收变换。MLA 对于 qi\boldsymbol{q}_i 和 ki\boldsymbol{k}_i 的处理略有不同，前者正常训练 hh 个 Wqr(s)\boldsymbol{W}_{qr}^{(s)}，后者却借用了 MQA 的思想全局共享一个 Wkr\boldsymbol{W}_{kr}（即 ki=xiWkrRi\boldsymbol{k}_i=\boldsymbol{x}_i\boldsymbol{W}_{kr}{\boldsymbol{\mathcal{R}}_i}），这样能尽可能降低新引入的 drd_r 个维度的 K Cache。

标准 MLA

标准的 MLA 结构（吸收变换前）如下。有两个需要注意的点：

  • 计算 qi(s)\boldsymbol{q}_i^{(s)} 时模仿了 ki(s)\boldsymbol{k}_i^{(s)} 的方式引入了 ci′\boldsymbol{c}_i' 降维，这一步和减少 KV Cache 无关。猜测是想前向时缓存 ci′\boldsymbol{c}_i'。
  • 计算 ki(s)\boldsymbol{k}_i^{(s)} 时两个部分左乘的两个向量不一致，右边仍然保持 xi\boldsymbol{x}_i，可能 RoPE 时想尽可能保持原向量。

ot=[ot(1),ot(2),⋯ ,ot(h)]ot(s)=Attention(qt(s),k≤t(s),v≤t(s))≜∑i≤texp⁡(qt(s)ki(s)⊤)vi(s)∑i≤texp⁡(qt(s)ki(s)⊤)qi(s)=[ci′Wqc(s),ci′Wqr(s)Ri]∈Rdk+dr,Wqc(s)∈Rdc′×dk,Wqr(s)∈Rdc′×drki(s)=[ciWkc(s),xiWkrRi]∈Rdk+dr,Wkc(s)∈Rdc×dk,Wkr∈Rd×drvi(s)=ciWv(s)∈Rdv,Wv(s)∈Rdc×dvci′=xiWc′∈Rdc′,Wc′∈Rd×dc′ci=xiWc∈Rdc,Wc∈Rd×dc\begin{equation} \begin{gathered} \boldsymbol{o}_t = \left[\boldsymbol{o}_t^{(1)}, \boldsymbol{o}_t^{(2)}, \cdots, \boldsymbol{o}_t^{(h)}\right] \\[10pt] \boldsymbol{o}_t^{(s)} = Attention\left(\boldsymbol{q}_t^{(s)}, \boldsymbol{k}_{\leq t}^{(s)} ,\boldsymbol{v}_{\leq t}^{(s)}\right)\triangleq\frac{\sum_{i\leq t}\exp\left(\boldsymbol{q}_t^{(s)} \boldsymbol{k}_i^{(s)}{}^{\top}\right)\boldsymbol{v}_i^{(s)}}{\sum_{i\leq t}\exp\left(\boldsymbol{q}_t^{(s)} \boldsymbol{k}_i^{(s)}{}^{\top}\right)} \\[15pt] \boldsymbol{q}_i^{(s)} = \left[\boldsymbol{c}_i'\boldsymbol{W}_{qc}^{(s)}, \boldsymbol{c}_i'\boldsymbol{W}_{qr}^{(s)}{\boldsymbol{\mathcal{R}}_i}\right]\in\mathbb{R}^{d_k + d_r},\quad \boldsymbol{W}_{qc}^{(s)}\in\mathbb{R}^{d_c'\times d_k},\boldsymbol{W}_{qr}^{(s)}\in\mathbb{R}^{d_c'\times d_r}\\ \boldsymbol{k}_i^{(s)} = \left[\boldsymbol{c}_i\boldsymbol{W}_{kc}^{(s)}, \boldsymbol{x}_i\boldsymbol{W}_{kr}{\boldsymbol{\mathcal{R}}_i}\right]\in\mathbb{R}^{d_k+d_r},\quad \boldsymbol{W}_{kc}^{(s)}\in\mathbb{R}^{d_c\times d_k}, \boldsymbol{W}_{kr}\in\mathbb{R}^{d\times d_r} \\ \boldsymbol{v}_i^{(s)} = \boldsymbol{c}_i\boldsymbol{W}_v^{(s)}\in\mathbb{R}^{d_v},\quad \boldsymbol{W}_v^{(s)}\in\mathbb{R}^{d_c\times d_v} \\[10pt] \boldsymbol{c}_i' = \boldsymbol{x}_i \boldsymbol{W}_c'\in\mathbb{R}^{d_c'},\quad \boldsymbol{W}_c'\in\mathbb{R}^{d\times d_c'} \\ \boldsymbol{c}_i = \boldsymbol{x}_i \boldsymbol{W}_c\in\mathbb{R}^{d_c},\quad \boldsymbol{W}_c\in\mathbb{R}^{d\times d_c} \\ \end{gathered} \end{equation}

经过吸收变换后的 MLA 结构如下：

ot=[ot(1)Wv(1),ot(2)Wv(2),⋯ ,ot(h)Wv(h)]ot(s)=Attention(qt(s),k≤t,c≤t)≜∑i≤texp⁡(qt(s)ki⊤)ci∑i≤texp⁡(qt(s)ki⊤)qi(s)=[ci′Wqc(s)Wkc(s)⊤,ci′Wqr(s)Ri]∈Rdc+drki=[ci,xiWkrRi]∈Rdc+drWqc(s)∈Rdc′×dk,Wkc(s)∈Rdc×dk,Wqr(s)∈Rdc′×dr,Wkr∈Rd×drci′=xiWc′∈Rdc′,Wc′∈Rd×dc′ci=xiWc∈Rdc,Wc∈Rd×dc\begin{equation} \begin{gathered} \boldsymbol{o}_t = \left[\boldsymbol{o}_t^{(1)}\boldsymbol{W}_v^{(1)}, \boldsymbol{o}_t^{(2)}\boldsymbol{W}_v^{(2)}, \cdots, \boldsymbol{o}_t^{(h)}\boldsymbol{W}_v^{(h)}\right] \\[10pt] \boldsymbol{o}_t^{(s)} = Attention\left(\boldsymbol{q}_t^{(s)}, \boldsymbol{k}_{\leq t} ,\boldsymbol{c}_{\leq t}\right)\triangleq\frac{\sum_{i\leq t}\exp\left(\boldsymbol{q}_t^{(s)} \boldsymbol{k}_i{}^{\top}\right)\boldsymbol{c}_i}{\sum_{i\leq t}\exp\left(\boldsymbol{q}_t^{(s)} \boldsymbol{k}_i{}^{\top}\right)} \\[15pt] \boldsymbol{q}_i^{(s)} = \left[\boldsymbol{c}_i'\boldsymbol{W}_{qc}^{(s)}\boldsymbol{W}_{kc}^{(s)}{}^{\top}, \boldsymbol{c}_i'\boldsymbol{W}_{qr}^{(s)}{\boldsymbol{\mathcal{R}}_i}\right]\in\mathbb{R}^{d_c + d_r}\\ \boldsymbol{k}_i = \left[\boldsymbol{c}_i, \boldsymbol{x}_i\boldsymbol{W}_{kr}{\boldsymbol{\mathcal{R}}_i}\right]\in\mathbb{R}^{d_c+d_r}\\ \boldsymbol{W}_{qc}^{(s)}\in\mathbb{R}^{d_c'\times d_k},\boldsymbol{W}_{kc}^{(s)}\in\mathbb{R}^{d_c\times d_k},\boldsymbol{W}_{qr}^{(s)}\in\mathbb{R}^{d_c'\times d_r},\boldsymbol{W}_{kr}\in\mathbb{R}^{d\times d_r} \\[10pt] \boldsymbol{c}_i' = \boldsymbol{x}_i \boldsymbol{W}_c'\in\mathbb{R}^{d_c'},\quad \boldsymbol{W}_c'\in\mathbb{R}^{d\times d_c'} \\ \boldsymbol{c}_i = \boldsymbol{x}_i \boldsymbol{W}_c\in\mathbb{R}^{d_c},\quad \boldsymbol{W}_c\in\mathbb{R}^{d\times d_c} \\ \end{gathered} \end{equation}

在 DeepSeek V3 671B 的配置中，d=7168,dc′=1536,dc=512,dk=dv=128,dr=64d=7168,d_c'=1536,d_c=512,d_k=d_v=128,d_r=64。

V3 推理代码

DeepSeek V3 推理代码详见其开源的 Github。

MLA 层

【待施工】

图源：河小涌 DeepSeek-v3代码demo解读：架构与推理！

DeepEP 源码

不自量力地分析一下 DeepEP 的开源代码。网上找到 zartbot 和 Qzhangyu 的两份资料，仍觉不够详细。

公共函数和变量

变量 含义
threadIdx.x 当前线程在线程块中的 x 坐标，范围 [0,blockDim.x-1][0, \text{blockDim.x-1}]
blockIdx.x 当前线程块在网格中的 x 坐标，范围 [0,gridDim.x−1][0, \text{gridDim.x} - 1]
blockDim.x 当前线程块在 x 方向的线程数
gridDim.x 当前网格在 x 方向的线程块数
channel 每两个 SM 构成一个 channel，偶数用于发送，奇数用于接收
前缀用法 含义
__device__ 定义设备（GPU）级别的共享内存
__global__ 声明一个 CUDA 的内核函数，由 CPU 调用、GPU 执行
__managed__ 定义统一内存，可以同时被 CPU 和 GPU 的所有线程访问
__shared__ 定义线程块级别的共享内存
不同的同步机制 含义
__syncwarp() 同步当前线程束内的所有线程
__syncthreads() 同步当前线程块内的所有线程
bar.sync(%1, %2)
value_1 = __shfl_sync(0x????????, value_2, lane_id, width=32) 将当前线程束里的线程 lane_id 的数值 value_2 广播给满足掩码的其他线程
__any_sync(0xffffffff, true/false) 当前线程束里满足掩码的任意线程返回真则结果为真

函数或编译器指令：

函数名 含义
__launch_bounds__(kNumThreads, 1) 指定每个线程块里的线程数，和每个 SM 上驻留的线程块数
__ldg() 从 GPU 的全局内存里读取数据，并用只读缓存加速

warp_reduce_sum 这个函数用来将同一个线程束里所有线程的值进行求和：

1
2
3
4
5
6
7
8
__forceinline__ __device__ int warp_reduce_sum(int value) {
    value += __shfl_xor_sync(0xffffffff, value, 16);
    value += __shfl_xor_sync(0xffffffff, value, 8);
    value += __shfl_xor_sync(0xffffffff, value, 4);
    value += __shfl_xor_sync(0xffffffff, value, 2);
    value += __shfl_xor_sync(0xffffffff, value, 1);
    return value;
}

【TODO】

1
2
3
CUDA_CHECK(cudaMallocHost(&moe_recv_counter, sizeof(int64_t), cudaHostAllocMapped));
CUDA_CHECK(cudaHostGetDevicePointer(&moe_recv_counter_mapped, const_cast<int*>(moe_recv_counter), 0));
    *moe_recv_counter = -1;

intranode 代码梳理

变量定义：

  • per_rank_buffer：[rank][i,j] 记录了设备 i 要向设备 j 发送的 tokens 数量（每个 rank 都是统一的）。
  • per_expert_buffer：[rank][i,j] 记录了设备 rank 要向设备 i 上的专家 j 发送的 token 数量。

91 行 dst_rank 不会缺少或溢出吗？没有做任何处理。

目标（对于每一个 GPU）

  • Buffer.rank_prefix_matrix[i,j] 表示编号为 0~i 的 GPU 向编号为 j 的 GPU 要发送的 token 的数量之和，其中 Buffer.moe_recv_counter_mapped 记录了到本 GPU 之和。
  • Buffer.moe_recv_expert_counter_mapped[j]：本 GPU 的第 j 个专家总共要接收多少 token（对齐到 expert_alignment 的倍数）。
  • Buffer.channel_prefix_matrix[i,j] 表示本 GPU 要往设备 i 发送的 token 中，归属于 channel 0~j 的数量的前缀和。

注意有 __launch_bounds__ 声明，把每个线程块的线程数固定在了 512，且 SM 和线程块可视为一一对应（下面的 sm_id=blockIdx.x 的写法用到了这一性质）。knumRanks 是机器内 GPU 数量，可视为 8。

我对 responsible_rank=thread_id / num_threads_per_rank 的式子琢磨了好久，疑问是 thread_id 明明是线程块里的唯一线程标识，为何看起来像是横跨机器内 8 个 GPU 的线程唯一标识。后来想通了，thread_id 的定义没有发生变化，只是说将当前线程块里的线程按照 GPU 数量划分了，每部分负责发送/接收对应 GPU。

1
2
3
4
5
6
7
__global__ void __launch_bounds__(kNumThreads=512, 1)
const auto num_sms = static_cast<int>(gridDim.x), sm_id = static_cast<int>(blockIdx.x);
const auto thread_id = static_cast<int>(threadIdx.x);
// Several warps are response for a single rank
const auto num_threads_per_rank = kNumThreads / responsible_rank;
const auto num_channels = num_sms / 2;
const auto responsible_rank = (static_cast<int>(thread_id)) / num_threads_per_rank;