这是 Professor Bo Li 推荐我的一篇 paper，有关 Adversarial Attacks 的内容，Arxiv 传送门。

什么是 Sensing-Reasoning pipelines

  • 对于 Sensing 层面，我们用若干种不同的模型去感知，得到很多组 0101 的随机变量。
  • 对于 Reasoning 层面，我们把之前的若干个结果汇总，利用领域知识（domain knowledge）和概率模型去矫正和逼近真实答案。常见的概率模型有：
    • 基于无向图的 Markov logic networks（MLN）
    • 基于有向图的 Bayesian networks （其实就是条件概率构建在图上）
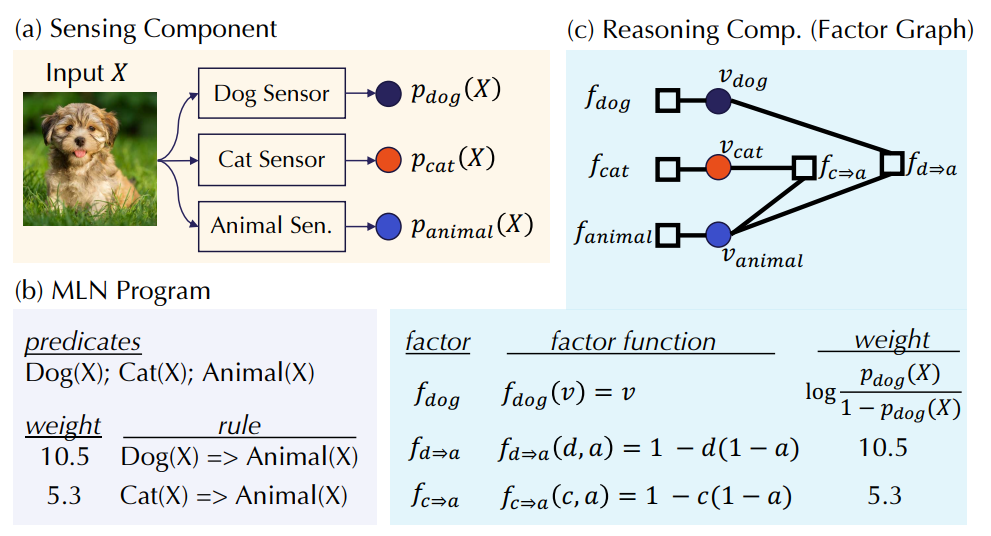
  • 论文里介绍了一个有趣的例子：假设我们想判断一张图 XX 的信息。
    • 我们在 Sensing 层面设了 Dog Sensor，Cat Sensor 和 Animial Sensor 三个神经网络模型去感知，从而能得到三个概率 p1,p2,p3p_1, p_2, p_3，pip_i 表示该图 是 物体 ii 的概率。
    • 由知识和经验，我们知道猫和狗都是动物，该规律可以在 Reasoning 层面帮我们去矫正之前的概率。

Markov Logic Networks

  • 下面介绍一下在 Reasoning 层面下的 MLN 的标准化定义。它是一张图 (V,F)\mathcal{(V,F)} 。
    • V=X∪Y\mathcal{V=X \cup Y} 代表节点集合。
      • X\mathcal{X} 是为每一个 Sensor 分别创立的点的集合，Y\mathcal{Y} 是 MLN 里的其他节点集合。
    • F=G∪H\mathcal{F=G \cup H} 代表事实集合，每个元素 ff 包括权重 wfw_f 和函数 FfF_f（从 V\mathcal{V} 的一个子集映射到 {0,1}\{0,1\}）
      • G\mathcal{G} 对应 X\mathcal{X} 子集里每一个点的 Factor，wGi=log⁡pi(X)1−pi(X)w_{G_i}=\log{\frac{p_i(X)}{1-p_i(X)}}，FGi(a)=[a=1]F_{G_i}(a)=[a=1]
      • H\mathcal{H} 对应 MLN 里的其他 Factor 集合。
  • 对于任何一个可能的情况，MLN 里的每一个节点都会有一个唯一的 00 或 11 的取值，我们称它为一个 possible world。更规范地来说，一个 possible world 对应一个函数 σ:V→{0,1}\sigma:\mathcal{V} \rightarrow \{0,1\}
  • 一个 MLN 节点的最终预测由以下公式给出
    • E[RMLN({pi(X)}i∈[n])]=Pr⁡[v=1]=Z1({pi(X)}i∈[n])Z2({pi(X)}i∈[n])\mathbb{E}[R_{M L N}(\{p_{i}(X)\}_{i \in[n]})]=\operatorname{Pr}[v=1] = \frac{Z_{1}(\{p_{i}(X)\}_{i \in[n]})}{Z_{2}(\{p_{i}(X)\}_{i \in[n]})}
    • Z1({pi(X)}i∈[n])=∑σ∈Σ∧σ(v)=1exp⁡{∑Gi∈GwGiσ(xi)+∑H∈HwHfH(σ(v‾H))}Z_{1}(\{p_{i}(X)\}_{i \in[n]})=\sum \limits_{\sigma \in \Sigma \wedge \sigma(v)=1} \exp \{\sum_{G_{i} \in \mathcal{G}} w_{G_{i}} \sigma(x_{i})+\sum_{H \in \mathcal{H}} w_{H} f_{H}(\sigma(\overline{\mathbf{v}}_{H}))\}
    • Z2({pi(X)}i∈[n])=∑σ∈Σexp⁡{∑Gi∈GwGiσ(xi)+∑H∈HwHfH(σ(v‾H))}Z_{2}(\{p_{i}(X)\}_{i \in[n]})=\sum \limits_{\sigma \in \Sigma} \exp \{\sum_{G_{i} \in \mathcal{G}} w_{G_{i}} \sigma(x_{i})+\sum_{H \in \mathcal{H}} w_{H} f_{H}(\sigma(\overline{\mathbf{v}}_{H}))\}
  • 这里也可以解释为什么 G\mathcal{G} 集合里的 Factor 权重要定义为 log⁡pi(X)1−pi(X)\log{\frac{p_i(X)}{1-p_i(X)}}，因为假设 H=∅\mathcal{H}=\varnothing，把这个式子带入预测公式，得到的答案正好是 pi(X)p_i(X)，这是自洽、符合逻辑的。

Reasoning Robustness 的复杂性理论

  • Counting Problem：给出多项式时间内可计算的权值函数 ww 和询问函数 QQ（相当于一个模型，比如可以用 MLN） 以及一个实数 εc>0\varepsilon_c>0，要 求一个Z 使得 1−εc≤ZEσ∼πα[Q(σ)]≤1+εc1-\varepsilon_{c} \leq \frac{Z}{\mathbf{E}_{\sigma \sim \pi_{\alpha}}[Q(\sigma)]} \leq 1+\varepsilon_{c}
  • Robustness Problem：给出多项式时间内可计算的权值函数 ww 和询问函数 QQ 以及两个实数 ϵ,δ>0\epsilon,\delta>0，对于满足 ∣α−α′∣∞<ϵ|\alpha-\alpha'|_{\infty} < \epsilon 的任何扰动 α′\alpha' ，判定 是否一直有 ∣Eσ∼πα[Q(σ)]−Eσ∼πα′[Q(σ)]∣<δ|\mathbf{E}_{\sigma \sim \pi_{\alpha}}[Q(\sigma)]-\mathbf{E}_{\sigma \sim \pi_{\alpha^{\prime}}}[Q(\sigma)]|<\delta 。

*Counting 到 Robustness 的规约

  • 论文里证明了：COUNTING 问题可以通过询问 O(1εC2)O(\frac{1}{\varepsilon_C^2}) 次 规约到 ROBUSTNESS 问题。

    • 我们要解决的 COUNTING 问题是：求 Eσ∼πα[Q(σ)]=Z1Z0+Z1\mathbf{E}_{\sigma \sim \pi_{\alpha}}[Q(\sigma)]=\frac{Z_{1}}{Z_{0}+Z_{1}}
    • 设计一个去 ROBUSTNESS 里询问的新问题，它的权重函数为 t(σ;β)=w(σ;α)exp⁡(βQ(σ))t(\sigma ; \beta)=w(\sigma ; \alpha) \exp (\beta Q(\sigma)) ，其中 w,Qw,Q 是原 COUNTING 问题的参数，α\alpha 是原分布，β\beta 是新分布。
    • 则这个新问题满足 Eσ∼τβ[Q(σ)]=eβZ1Z0+eβZ1\mathbf{E}_{\sigma \sim \tau_{\beta}}[Q(\sigma)]=\frac{e^{\beta} Z_{1}}{Z_{0}+e^{\beta} Z_{1}}

  • 设 R=Z0Z1R=\frac{Z_0}{Z_1}，我们来评估分布 β\beta 偏差了一个 xx 后函数值的变化：

    • Y+(β,x)=Eσ∼τβ+x[Q(σ)]−Eσ∼τβ[Q(σ)]=exeβZ1Z0+exeβZ1−eβZ1Z0+eβZ1=(ex−1)eβR+(ex+1)eβ+exe2βRY^{+}(\beta, x)=\mathbf{E}_{\sigma \sim \tau_{\beta+x}}[Q(\sigma)]-\mathbf{E}_{\sigma \sim \tau_{\beta}}[Q(\sigma)]=\frac{e^{x} e^{\beta} Z_{1}}{Z_{0}+e^{x} e^{\beta} Z_{1}}-\frac{e^{\beta} Z_{1}}{Z_{0}+e^{\beta} Z_{1}}=\frac{(e^{x}-1) e^{\beta}}{R+(e^{x}+1) e^{\beta}+\frac{e^{x} e^{2 \beta}}{R}}
    • Y−(β,x)=Eσ∼τβ[Q(σ)]−Eσ∼τβ−x[Q(σ)]=eβZ1Z0+eβZ1−e−xeβZ1Z0+e−xeβZ1=(ex−1)eβexR+(ex+1)eβ+e2βRY^{-}(\beta, x)=\mathbf{E}_{\sigma \sim \tau_{\beta}}[Q(\sigma)]-\mathbf{E}_{\sigma \sim \tau_{\beta-x}}[Q(\sigma)]=\frac{e^{\beta} Z_{1}}{Z_{0}+e^{\beta} Z_{1}}-\frac{e^{-x} e^{\beta} Z_{1}}{Z_{0}+e^{-x} e^{\beta} Z_{1}}=\frac{(e^{x}-1) e^{\beta}}{e^{x} R+(e^{x}+1) e^{\beta}+\frac{e^{2 \beta}}{R}}
    • 上述两式均 ≤ex/2−1ex/2+1\leq \frac{e^{x / 2}-1}{e^{x / 2}+1}，且在 R=eβ±x/2R=e^{\beta \pm x / 2} 时取到。
    • 设 Y(β)=max⁡{Y+(β,x),Y−(β,x)}Y(\beta)=\max \{Y^{+}(\beta, x), Y^{-}(\beta, x)\}，则 Y(β)Y(\beta) 由 eβe^{\beta} 和 RR 的大小关系决定。
    • YY 函数满足：在 [0,log⁡R−x/2][0, \log R-x / 2] 上升，[log⁡R−x/2,log⁡R][\log R-x / 2, \log R] 下降，[log⁡R,log⁡R+[\log R, \log R+ x/2]x / 2] 上升, [log⁡R+x/2,∞)[\log R+x / 2, \infty) 下降。

  • **我们希望用 ROBUSTNESS 的结果估计 RR，这样 COUNTING 问题的答案就是 Eσ∼πα[Q(σ)]=11+R\mathbf{E}_{\sigma \sim \pi_{\alpha}}[Q(\sigma)]=\frac{1}{1+R} **

    1. 假设 xx 是一个已知的 O(εc)O(\varepsilon_{c}) 的定值
    2. 首先，如果分布 β\beta 已经确定，我们可以二分 δ\delta + 调用判定，求出误差小于 εc\varepsilon_{c} 的 δ\delta，也即 Y(β)Y(\beta) 的值。
    3. 我们已经知道了 YY 函数的性质，可以再套一个二分去找极大值点 β0\beta_0，使得 Y(β0)≥ex/2−1ex/2+1−ε0Y(\beta_{0}) \geq \frac{e^{x / 2}-1}{e^{x / 2}+1}-\varepsilon_{0}。
    4. 根据一番推导，我们找到的这个 β0\beta_0 满足 e−x<Reβ0<exe^{-x}<\frac{R}{e^{\beta_{0}}}<e^{x}，这样我们便确定了 RR 的范围。
    5. 最后我们只要设 x=log⁡(1+εc)x=\log(1+\varepsilon_{c})，那么估计值 11+R\frac{1}{1+R} 的偏差就是 εc\varepsilon_{c} 了。