朝花夕拾·漫谈高中
记录了高中校园生活的记忆片段。
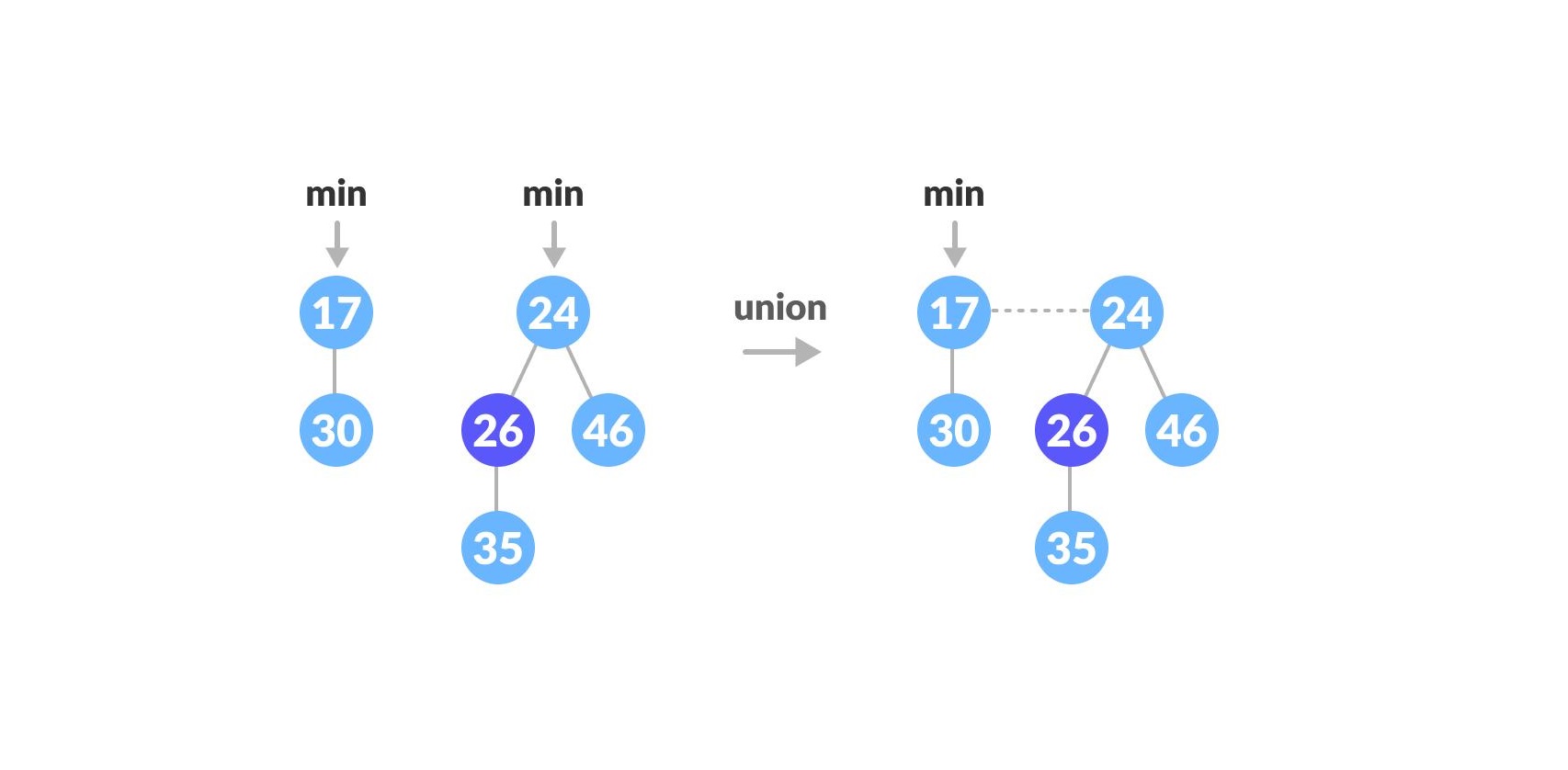
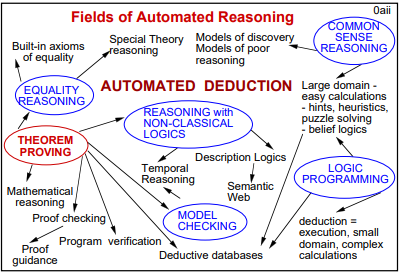
算法的设计和分析
记录了我 2020.4-2020.6 在浙江大学上的《算法设计与分析》这门课的知识点。我会挑一些新奇有趣的、以前没见过的主题进行分享,可以把这篇文章和趣题摘记系列结合起来看。
冒险动漫推荐
该博客记录了我看过的冒险、剧情类的动漫(动画/电影)。我为每部动漫都配上图片和简要评价,略有剧透。
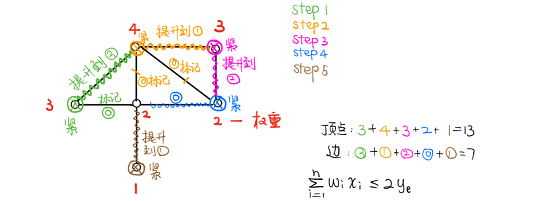
应用运筹学-线性规划应用
我在大三春夏学期上了张国川老师的《应用运筹学基础》这门课。张国川老师坚持板书讲解,课上干货满满,这篇文章是三分之一的课程笔记。
CoSQL 数据集
记录了我 2020.3-2020.6 在浙江大学上的《机器学习》这门课的知识点。
2021华为软件精英挑战赛总结
记录了我 2021.03.10~2021.04.24 获得华为软件精英挑战赛全球季军的比赛历程。
2021 数智马拉松大赛
记录了我 2021.9 获得数智马拉松一等奖的比赛历程。
Docker
记录了 Docker 相关的工程知识。
Django 学习笔记
记录了我 2020.3-2020.6 在浙江大学上的《BS体系软件设计》这门课的课程设计所用到的后端知识点。
趣题摘记-奇思妙想
记录了数学和计算机领域,通过小小思考后能豁然开朗的趣题。